
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
【答案】B
【解析】
试题分析:根据抛物线的对称轴为直线x=﹣![]() =2,则有4a+b=0;观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时,y随x的增大而减小.
=2,则有4a+b=0;观察函数图象得到当x=﹣3时,函数值小于0,则9a﹣3b+c<0,即9a+c<3b;由于x=﹣1时,y=0,则a﹣b+c=0,易得c=﹣5a,所以8a+7b+2c=8a﹣28a﹣10a=﹣30a,再根据抛物线开口向下得a<0,于是有8a+7b+2c>0;由于对称轴为直线x=2,根据二次函数的性质得到当x>2时,y随x的增大而减小.
解:∵抛物线的对称轴为直线x=﹣![]() =2,
=2,
∴b=﹣4a,即4a+b=0,(故①正确);
∵当x=﹣3时,y<0,
∴9a﹣3b+c<0,
即9a+c<3b,(故②错误);
∵抛物线与x轴的一个交点为(﹣1,0),
∴a﹣b+c=0,
而b=﹣4a,
∴a+4a+c=0,即c=﹣5a,
∴8a+7b+2c=8a﹣28a﹣10a=﹣30a,
∵抛物线开口向下,
∴a<0,
∴8a+7b+2c>0,(故③正确);
∵对称轴为直线x=2,
∴当﹣1<x<2时,y的值随x值的增大而增大,
当x>2时,y随x的增大而减小,(故④错误).
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场购进一批日用品,若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数![]() (件)与价格
(件)与价格![]() (元/件)之间满足一次函数关系.
(元/件)之间满足一次函数关系.
(1)试求:y与x之间的函数关系式;
(2)这批日用品购进时进价为4元,则当销售价格定为多少时,才能使每月的润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连结OE.下列结论:
BC,连结OE.下列结论:
①∠CAD=30°;②SABCD=AB·AC;③OB=AB;④OE=![]() BC,成立的结论有______.(填序号)
BC,成立的结论有______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
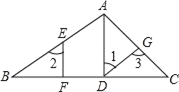
【题目】如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南市地铁1号线于2019年1月1日起正式通车,在修建过程中,技术人员不断改进技术,提高工作效率,如在打通一条长600米的隧道时,计划用若干小时完成,在实际工作过程中,每小时打通隧道长度是原计划的1.2倍,结果提前2小时完成任务.
(1)求原计划每小时打通隧道多少米?
(2)如果按照这个速度下去,后面的360米需要多少小时打通?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
①![]() 的解x= .
的解x= .
②![]() 的解x= .
的解x= .
③![]() 的解x= .
的解x= .
④![]() 的解x= .
的解x= .
…
(1)根据你发现的规律直接写出⑤,⑥个方程及它们的解.
(2)请你用一个含正整数n的式子表示上述规律,并求出它的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,点D在BC上,且AD=AE.
(1)若∠BAC=90°,∠BAD=30°,求∠EDC的度数?
(2)若∠BAC=a(a>30°),∠BAD=30°,求∠EDC的度数?
(3)猜想∠EDC与∠BAD的数量关系?(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD//EF,∠1+∠2=180°,
(1)若∠1=50°,求∠BAD的度数;
(2)若DG⊥AC,垂足为G,∠BAC=90°,试说明:DG平分∠ADC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com