
分析 由a-b=2可得b=a-2,代入$\frac{1}{a+1}+\frac{2}{b}$变为只含有a的代数式,由2a2+a-4=0可得${a}^{2}=\frac{-a+4}{2}$,再代入前面化简后的式子,即可解答本题.
解答 解:∵a-b=2,
∴b=a-2.
∴$\frac{1}{a+1}+\frac{2}{b}$=$\frac{1}{a+1}$+$\frac{2}{a-2}$=$\frac{a-2+2a+2}{{a}^{2}-a-2}$=$\frac{3a}{{a}^{2}-a-2}$.
∵2a2+a-4=0,
∴${a}^{2}=\frac{-a+4}{2}$.
∴$\frac{3a}{{a}^{2}-a-2}$=$\frac{3a}{\frac{-a+4}{2}-a-2}=\frac{6a}{-a+4-2a-4}=\frac{6a}{-3a}=-2$.
故答案为:-2.
点评 本题考查分式的化简求值,解题的关键是可以将题目中的式子灵活变化,变为所求式子需要的条件


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
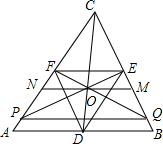 如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.
如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
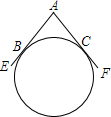 一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径.
一个圆形工件与两条直尺AE、AF按如图所示的方式放置在一起,所成的夹角为∠EAF=120°,设圆形工件分别与AE、AF相切于点B、C.小明想用刻度尺测量这个圆形工件的直径,但发现刻度尺的长度稍短些.请你设计两种不同的测量方法,仍用这把刻度尺并结合简单的计算,测出这个工件的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com