
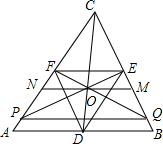
 如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.
如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ. 分析 先由DN与DM是角平分线可推出$\frac{CN}{AN}=\frac{CM}{BM}$,即MN∥AB,而EF∥AB,从而MN∥EF,得出线段比例关系,推与PQ∥EF∥MN∥AB,即四线平行;过点C作CG∥AB,交DM的延长于点G,可证CG=CD,即:将线段CD转移成CG,从而只需证CG=PQ即可,而此时五线平行,显然利用推导线段比例关系得出结论.
解答 证明:如图: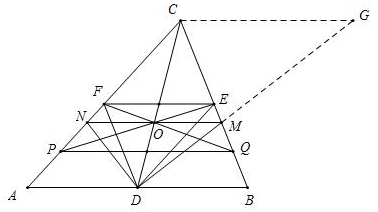
∵DN平分∠ADC,
∴$\frac{CN}{AN}=\frac{CD}{AD}$,
同理$\frac{CM}{BM}=\frac{CD}{BD}$,
∵BD=AD,
∴$\frac{CN}{AN}=\frac{CM}{BM}$,
∴MN∥AB,
∴$\frac{ON}{AD}=\frac{CO}{CD}=\frac{OM}{BD}$,
∴ON=OM,
∵E、F分别是AC、BC的中点,
∴EF∥AB,EF=AD=BD,
∴EF∥MN,
∴$\frac{ON}{EF}=\frac{OP}{PE}$,$\frac{OM}{EF}=\frac{OQ}{FQ}$,
∴$\frac{PO}{PE}=\frac{QO}{QF}$,
∴PQ∥EF∥MN∥AB,
过点C作CG∥AB交DM的延长线于点G,如图,
∴∠CGD=∠GDB,
∵∠CDG=∠GDB,
∴∠CDG=∠CGD,
∴CD=CG,
∵$\frac{OM}{CG}=\frac{OD}{CD}$,$\frac{OM}{BD}=\frac{OC}{CD}$,
∴$\frac{OM}{CG}+\frac{OM}{BD}=\frac{OD}{CD}+\frac{OC}{CD}=\frac{CD}{CD}=1$,
又∵$\frac{ON}{EF}=\frac{PN}{PF}$,$\frac{ON}{PQ}=\frac{FN}{FP}$
∴$\frac{ON}{EF}+\frac{ON}{PQ}=\frac{PN}{PF}+\frac{NF}{PF}=\frac{PF}{PF}=1$,
∵OM=ON,EF=BD,
∴CG=PQ,
∵CG=CD,
∴CD=PQ.
点评 本题考查了三角形的中位线定理、平行线分线段成比例定理及其逆定理、相似三角形判定与性质、角平分线的性质、角平分线比例定理、等腰三角形的判定与性质等多个知识点,难度很大,是一道偏竞赛的几何证明题.要证两条线段相等,若直接证不好证,则想办法转移其中一条或两条同时转移,本题利角平分线和平行线构造等腰三角形,从而将CD转移成CG使问题得以突破.另外,熟练地使用平行线分线段成比例定理进行线段比例等式的恒等变形也是本题的关键和难点所在.此题可以作为一个经典结论,希望同学们熟练掌握其推导过程,并能应用到其它几何证明中去.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:解答题
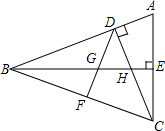 如图,CD和BE是△ABC的两条高,∠BCD=45°,BF=FC,BE与DF、DC分别交于点G、H,∠ACD=∠CBE.
如图,CD和BE是△ABC的两条高,∠BCD=45°,BF=FC,BE与DF、DC分别交于点G、H,∠ACD=∠CBE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7 | B. | -1 | C. | 19 | D. | -1或7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
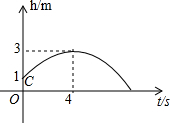 如图,铅球的出手点C距地面1米,出手后的运动路线是抛物线,出手后4秒钟达到最大高度3米,则铅球运行路线的解析式为h=-$\frac{1}{8}$(t-4)2+3或h=-$\frac{1}{8}$t2+t+1.
如图,铅球的出手点C距地面1米,出手后的运动路线是抛物线,出手后4秒钟达到最大高度3米,则铅球运行路线的解析式为h=-$\frac{1}{8}$(t-4)2+3或h=-$\frac{1}{8}$t2+t+1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等弧所对的圆心角相等 | |
| B. | 三角形的外心到这个三角形的三边距离相等 | |
| C. | 经过三点可以作一个圆 | |
| D. | 相等的圆心角所对的弧相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com