
分析 根据非负数的性质,可求出x、y的值,然后将代数式化简再代值计算.
解答 解:由(x+2)2+|x+y-2|=0,得
$\left\{\begin{array}{l}{x+2=0}\\{x+y-2=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$.
3x2y+{-2x2y-[-2xy+(x2y-4x2)]-xy}=3x2y+{-2x2y-[-2xy+x2y-4x2]-xy}
=3x2y+{-2x2y+2xy-x2y+4x2-xy}
=3x2y-2x2y+2xy-x2y-4x2+xy
=3xy-4x2,
当$\left\{\begin{array}{l}{x=-2}\\{y=4}\end{array}\right.$时,原式=3×(-2)×4-4×(-2)2=-24-16=-40.
点评 本题考查了整式的化简求值,利用非负数的和为零得出x、y的值是解题关键.


科目:初中数学 来源: 题型:解答题
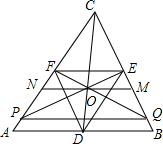 如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.
如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
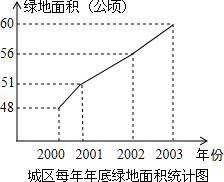 美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容.我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com