
分析 根据分式的加减乘除进行计算即可对原式化简,由a是2x2-2x-7=0的根,可知a符合这个方程,从而可以解答本题.
解答 解:$\frac{a-2}{{a}^{2}-1}$÷(a-1-$\frac{2a-1}{a+1}$)
=$\frac{a-2}{(a+1)(a-1)}÷\frac{(a-1)(a+1)-(2a-1)}{a+1}$
=$\frac{a-2}{(a+1)(a-1)}÷\frac{{a}^{2}-1-2a+1}{a+1}$
=$\frac{a-2}{(a+1)(a-1)}×\frac{a+1}{a(a-2)}$
=$\frac{1}{a(a-1)}$
=$\frac{1}{{a}^{2}-a}$.
∵a是2x2-2x-7=0的根,
∴2a2-2a-7=0.
∴${a}^{2}-a=\frac{7}{2}$.
∴原式=$\frac{1}{{a}^{2}-a}=\frac{1}{\frac{7}{2}}=\frac{2}{7}$.
点评 本题考查分式的化简求值,解题的关键是明确分式的加减乘除的法则,灵活变化,找出所求问题的条件.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 2014 | B. | 2015 | C. | $\frac{1}{2014}$ | D. | $\frac{1}{2015}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
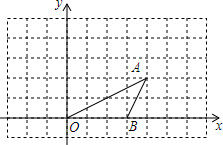 在边长为1的方格纸中建立直角坐标系,如图所示,O、A、B三点均为格点.
在边长为1的方格纸中建立直角坐标系,如图所示,O、A、B三点均为格点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知 a、b、c三数在数轴上的位置如图所示,其中|a|=|c|,化简:$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+|c|-|a|.
已知 a、b、c三数在数轴上的位置如图所示,其中|a|=|c|,化简:$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+|c|-|a|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
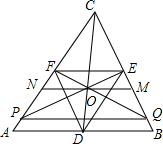 如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.
如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com