
【题目】阅读下列文字: 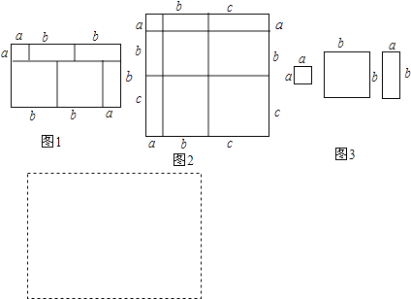
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2 .
请解答下列问题:
(1)写出图2中所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片, ①请按要求利用所给的纸片拼出一个几何图形,并画在图3所给的方框中,要求所拼出的几何图形的面积为2a2+5ab+2b2 ,
②再利用另一种计算面积的方法,可将多项式2a2+5ab+2b2分解因式.
【答案】
(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)解:a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc,
=112﹣2×38,
=45;
(3)①如图所示,
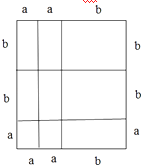
②如上图所示的矩形面积=(2a+b)(a+2b),
它是由2个边长为a的正方形、5个边长分别为a、b的长方形、2个边长为b的小正方形组成,所以面积为2a2+5ab+2b2,
则2a2+5ab+2b2=(2a+b)(a+2b),
故答案为:2a2+5ab+2b2=(2a+b)(a+2b).
【解析】(1)直接根据图形写出等式;(2)将所求式子与(1)的结论对比,得出变形的式子,代入求值即可;(3)①画出图形,答案不唯一,②根据原图形面积=组合后长方形的面积得出等式.
【考点精析】本题主要考查了因式分解的应用的相关知识点,需要掌握因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程才能正确解答此题.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,AD=2AB,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.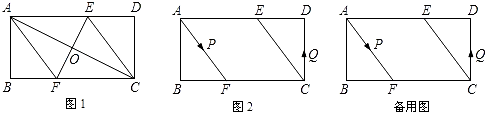
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒.当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值;
②若点P、Q的速度分别为v1、v2(cm/s),点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,试探究a与b满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
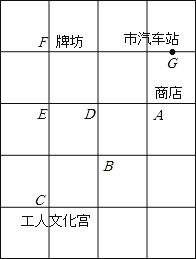
【题目】 如图是某市区四个景点或单位(A为商店,C为工人文化宫,F为牌坊,G为市汽车站)的大致平面图.可将方格的边长看作是一个单位长度.
(1)请你建立适当的直角坐标系,分别写出这四个地点的坐标.
(2)在商店A处有游客甲和游客乙,甲按线路A→D→E→F步行到达牌坊;乙按A→B→C步行到达工人文化宫,若一个单位长度代表100米,你能比较一下两人哪个走的路程较多吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
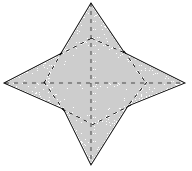
【题目】如图,把一个菱形绕着它的对角线的交点旋转90°,旋转前后的两个菱形构成一个“星形”(阴影部分),若菱形的一个内角为60°,边长为2,则该“星形”的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c图象上部分点的坐标满足下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣3 | ﹣2 | ﹣3 | ﹣6 | ﹣11 | … |
则该函数图象的顶点坐标为( )
A.(﹣3,﹣3)
B.(﹣2,﹣2)
C.(﹣1,﹣3)
D.(0,﹣6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并填空:
(1)为了求代数式 ![]() 的值,我们必须知道x的值.若x=1,则这个代数式的值为;若x=2,则这个代数式的值为 , ……可见,这个代数式的值因x的取值不同而变化.尽管如此,我们还是有办法来考虑这个代数式的值的范围.
的值,我们必须知道x的值.若x=1,则这个代数式的值为;若x=2,则这个代数式的值为 , ……可见,这个代数式的值因x的取值不同而变化.尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)把一个多项式进行部分因式分解可以解决求代数式的最大(或最小)值问题.例如: ![]() =(
=( ![]() )
) ![]() =
= ![]() ,因为
,因为 ![]() 是非负数,所以,这个代数式
是非负数,所以,这个代数式 ![]() 的最小值是 , 这时相应的x的平方是.
的最小值是 , 这时相应的x的平方是.
尝试探究并解答:
(3)求代数式 ![]() 的最小值,并写出相应x的值.
的最小值,并写出相应x的值.
(4)求代数式 ![]() 的最大值,并写出相应x的值.
的最大值,并写出相应x的值.
(5)已知 ![]() ,且x的值在数1~4(包含1和4)之间变化,试探求此时y的不同变化范围(直接写出当x在哪个范围变化时,对应y的变化范围).
,且x的值在数1~4(包含1和4)之间变化,试探求此时y的不同变化范围(直接写出当x在哪个范围变化时,对应y的变化范围).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com