练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】二次函数y=ax2+bx+c图象上部分点的坐标满足下表：

    x

    …

    ﹣3

    ﹣2

    ﹣1

    0

    1

    …

    y

    …

    ﹣3

    ﹣2

    ﹣3

    ﹣6

    ﹣11

    …

    则该函数图象的顶点坐标为（ ）
    A.（﹣3，﹣3）
    B.（﹣2，﹣2）
    C.（﹣1，﹣3）
    D.（0，﹣6）

    【答案】B
    【解析】解：∵x=﹣3和﹣1时的函数值都是﹣3相等， ∴二次函数的对称轴为直线x=﹣2，
    ∴顶点坐标为（﹣2，﹣2）．
    故选：B．
    【考点精析】根据题目的已知条件，利用二次函数的性质的相关知识可以得到问题的答案，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=BC，D、E、F分别是BC、AC、AB边上的中点．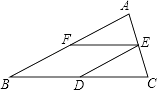
    （1）求证：四边形BDEF是菱形；
    （2）若AB=12cm，求菱形BDEF的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，∠B=90°，AB=8，DH=3，平移距离为4，求阴影部分的面积为（ ）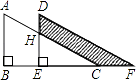
    A.20
    B.24
    C.25
    D.26

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列文字：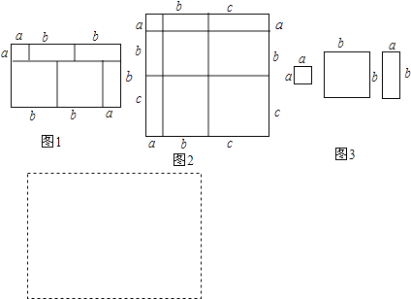
    我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式，例如由图1可以得到（a+2b）（a+b）=a2+3ab+2b2 ．
    请解答下列问题：
    （1）写出图2中所表示的数学等式；
    （2）利用（1）中所得到的结论，解决下面的问题：已知a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值；
    （3）图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片， ①请按要求利用所给的纸片拼出一个几何图形，并画在图3所给的方框中，要求所拼出的几何图形的面积为2a2+5ab+2b2 ，
    ②再利用另一种计算面积的方法，可将多项式2a2+5ab+2b2分解因式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在解方程3x－3＝2x－3时，小华同学是这样解的：

    方程两边同加上3，得3x－3＋3＝2x－3＋3.(1)

    于是3x＝2x.

    方程两边同除以x，得3＝2.(2)

    所以此方程无解．

    小华同学的解题过程是否正确？如果正确，请指出每一步的理由；如果不正确，请指出错在哪里，并加以改正．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（辽宁丹东）如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(1，4)，B(4，2)，C(3，5)（每个方格的边长均为1个单位长度）.

    （1）请画出△A1B1C1，使△A1B1C1与△ABC关于x轴对称；

    （2）将△ABC绕点O逆时针旋转90°，画出旋转后得到的△A2B2C2，并直接写出点B旋转到点B2所经过的路径长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】因式分解：3ab2+6ab+3a．

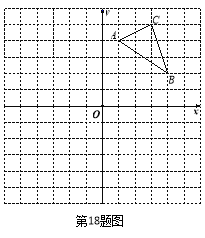
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们进入中学以来，已经学习过不少有关数据的统计量，例如_____________________等，它们分别从不同的侧面描述了一组数据的特征.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了抓住世博会商机，某商店决定购进A、B两种世博会纪念品，若购进A种纪念品10件，B种纪念品5件，需要1000元；若购进A种纪念品5件，B种纪念品3件，需要550元．
    （1）求购进A、B两种纪念品每件各需多少元？
    （2）若该商店决定拿出4000元全部用来购进这两种纪念品，考虑市场需求，要求购进A种纪念品的数量不少于B种纪念品数量的6倍，且不超过B钟纪念品数量的8倍，那么该商店共有几种进货方案？
    （3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少？

    查看答案和解析>>

    同步练习册答案