
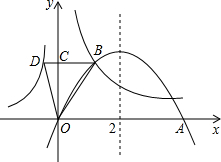
 如图,对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,与反比例函数y=
如图,对称轴为x=2的抛物线y=ax2+bx(a≠0)与x轴交于原点O与点A,与反比例函数y=| b |
| x |
| a |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
| b |
| x |
| a |
| x |
| b |
| x |
| a |
| x |
| b |
| y |
| a |
| y |
| BC |
| OC |
| b |
| y2 |
| a |
| y2 |


科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=| k |
| x |
| A、-2 | B、-4 | C、4 | D、-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、平行 | B、垂直 |
| C、相交 | D、无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5-a |
A、a≥-
| ||
| B、0<a≤5 | ||
C、-
| ||
| D、0<a≤5,且a≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
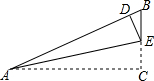 小明在学习“锐角三角函数”中发现,将如图的含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,这样就可以求出75°角的正切值是( )
小明在学习“锐角三角函数”中发现,将如图的含30°(∠BAC)角的直角三角形纸片ABC沿过点A的直线折叠,使点C落在AB上的点D处,这样就可以求出75°角的正切值是( )A、2-
| ||
B、2+
| ||
| C、2.5 | ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 甲 | 乙 | |
| 进价(元/部) | 4000 | 2500 |
| 售价(元/部) | 4300 | 3000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com