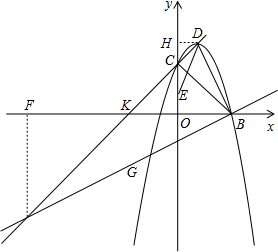
已知:在平面直角坐标系xOy中,二次函数y=-x2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,点A在x轴负半轴上,点B在x轴正半轴上,且CO=BO=3AO,AB=4,抛物线的顶点为D.
(1)求这个二次函数的解析式;
(2)点E(0,n)在y轴正半轴上,且位于点C的下方.当n在什么范围内取值时∠CBD<∠CED?当n在什么范围内取值时∠CBD>∠CED?
(3)若过点B的直线垂直于BD且与直线CD交于点P,求点P的坐标.
解:(1)设AO=m,
∵CO=BO=3AO,AB=4
∴CO=BO=3m,
∴m+3m=4,m=1
∴A、B、C的坐标分别为(-1,0),(3,0),(0,3),
∴二次函数的解析式为y=-x
2+2x+3;
(2)二次函数=-x
2+2x+3的顶点D的坐标为(1,4),
过点D作DH⊥y轴于H,
∴DH=1,CH=OH-OC=1
∴CD=

,
由题意,得BC=3

,BD=2

∴CD
2+BC
2=BD
2,
∴△BCD为直角三角形,
在Rt△BCD中,tan∠CBD=
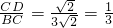
若∠CBD=∠CED,则tan∠CBD=tan∠CED
在Rt△EDH中,tan∠CED=
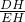
=

∴EH=3,
∴OE=1,
∴此时点E的坐标为(0,1),
∵点E位于点O的下方,
∴当1<n<3时,∠CBD<∠CED,
当0<n<1时,∠CBD>∠CED;
(3)∵△BCD为直角三角形,
∴BC⊥CD
∵过点B的直线垂直于BD且与直线CD交于点P
∴BP⊥BD
∴△BCD∽△PCB
∴BC
2=CD•PC,
∴PC=9

设直线CD的解析式为y=kx+b,
∵C点的坐标为(0,3),D坐标为(1,4)
∴直线CD的解析式为y=x+3,
∴直线CD与x轴交点K的坐标为(-3,0)
∴OC=OK=3,
∴∠CKO=∠FKP=45°,
∴CK=3

,
∴PK=6

过点P作PF⊥x轴于点F,
∴PF=6,FK=6,
∴P点的坐标为(-9,-6).
分析:(1)设AO=m,利用CO=BO=3AO,AB=4,得到CO=BO=3m,从而求得m的值后确定A、B、C的坐标分别为(-1,0),(3,0),(0,3),利用待定系数法确定二次函数的解析式即可;
(2)求得二次函数=-x
2+2x+3的顶点D的坐标,过点D作DH⊥y轴于H,利用DH=1,CH=OH-OC=1,得CD=

,得到CD
2+BC
2=BD
2,利用勾股定理的逆定理得到△BCD为直角三角形,利用锐角三角函数得到点E的坐标为(0,1),从而确定当1<n<3时,∠CBD<∠CED,
当0<n<1时,∠CBD>∠CED;
(3)根据△BCD为直角三角形,得到BC⊥CD,然后证得BCD∽△PCB,利用BC
2=CD•PC求得PC=9

,从而确定直线CD的解析式为y=x+3,然后求得CK=3

、PK=6

,过点P作PF⊥x轴于点F,得到PF=6,FK=6,从而确定P点的坐标为(-9,-6).
点评:本题考查了二次函数的综合知识,题目中涉及到了勾股定理的逆定理等知识,综合性较强,难度较大.

 解:(1)设AO=m,
解:(1)设AO=m, ,
, ,BD=2
,BD=2
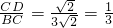
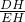 =
=

 ,
,
 ,得到CD2+BC2=BD2,利用勾股定理的逆定理得到△BCD为直角三角形,利用锐角三角函数得到点E的坐标为(0,1),从而确定当1<n<3时,∠CBD<∠CED,
,得到CD2+BC2=BD2,利用勾股定理的逆定理得到△BCD为直角三角形,利用锐角三角函数得到点E的坐标为(0,1),从而确定当1<n<3时,∠CBD<∠CED, ,从而确定直线CD的解析式为y=x+3,然后求得CK=3
,从而确定直线CD的解析式为y=x+3,然后求得CK=3 、PK=6
、PK=6 ,过点P作PF⊥x轴于点F,得到PF=6,FK=6,从而确定P点的坐标为(-9,-6).
,过点P作PF⊥x轴于点F,得到PF=6,FK=6,从而确定P点的坐标为(-9,-6).

 走进文言文系列答案
走进文言文系列答案
 如图,在平面直角坐标中,已知直线y=kx+b与直线y=
如图,在平面直角坐标中,已知直线y=kx+b与直线y= 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=