
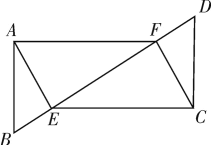
【题目】如图,AB∥CD,AB=CD,点E,F在BD上,∠BAE=∠DCF,连接AF,EC.
(1)求证:AE=FC;
(2)求证:四边形AECF是平行四边形.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)要证AE=CF,需证△ABE≌△CDF.由AB∥CD,可知∠B=∠D,又AB=CD,∠BAE=∠DCF,即可证得.
(2)由△ABE≌△CDF得AE=CF,∠AEB=∠CFD,故180°-∠AEB=180°-∠CFD,即∠AEF=∠CFE,AE∥CF,又AE=CF,故四边形AECF是平行四边形.
证明:(1)∵AB∥CD,
∴∠B=∠D.
在△ABE和△CDF中,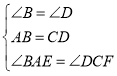
∴△ABE≌△CDF(ASA),
∴AE=FC.
(2)由(1)△ABE≌△CDF,得AE=CF,∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,即∠AEF=∠CFE,
∴AE∥CF.
∵AE=CF,
∴四边形AECF是平行四边形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:
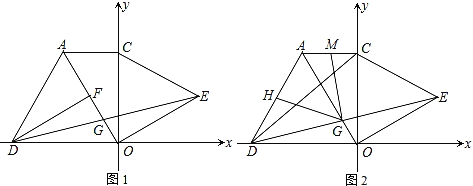
【题目】如图,在平面直角坐标系中,∠ACO=90°,∠AOC=30°,分别以AO、CO为边向外作等边三角形△AOD和等边三角形△COE,DF⊥AO于F,连DE交AO于G.
(1)求证:△DFG≌△EOG;
(2)H为AD的中点,连HG,求证:CD=2HG;
(3)在(2)的条件下,AC=4,若M为AC的中点,求MG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,四边形OABC是正方形,点A,C的坐标分别为(2,0),(0,2),D是x轴正半轴上的一点(点D在点A的右边),以BD为边向外作正方形BDEF(E,F两点在第一象限),连接FC交AB的延长线于点G.若反比例函数![]() 的图象经过点E,G两点,则k的值为 ______________.
的图象经过点E,G两点,则k的值为 ______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华文具用品店最近购进了一批钢笔,进价为每支6元,为了合理定价,在销售前4天试行机动价格,卖出时每支以10元为标准,超过10元的部分记为正,不足10元的部分记为负。文具店记录了这四天该钢笔的售价情况和售出情况,如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
每支价格相对标准价格(元) | +1 | 0 | -1 | -2 |
售出支数(支) | 12 | 15 | 32 | 33 |
(1)填空:这四天中赚钱最多的是第______天,这天赚了______元钱;
(2)求新华文具用品店这四天出售这种钢笔一共赚了多少钱;
(3)新华文具用品店准备用这四天赚的钱全部购进这种钢笔,进价仍为每支6元为了促销这种钢笔,每只钢笔的售价在10元的基础上打九折,本次购进的这种钢笔全部售出后共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.

A. 96 B. 204 C. 196 D. 304
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在线段AB上有一点C(点C不与A、B重合且AC>BC),分别以AC、BC为边作正方形ACED和正方形BCFG,其中点F在边CE上,连接AG.

(1)如图1,若AC=7,BC=5,则AG=______;
(2)如图2,若点C是线段AB的三等分点,连接AE、EG,求证:△AEG是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接全国文明城市的评选,市政府决定对春风路进行市政化改造,经过市场招标,决定聘请甲、乙两个工程队合作施工,已知春风路全长24千米,甲工程队每天施工的长度比乙工程队每天施工长度的多施工0.4千米,由甲工程队单独施工完成任务所需要的天数是乙工程队单独完成任务所需天数的![]() .
.
(1)求甲、乙两个工程队每天各施工多少千米?
(2)若甲工程队每天的施工费用为0.8万元,乙工程队每天的施工费用为0.5万元,要使两个工程队施工的总费用不超过7万元,则甲工程队至多施工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
(1)其图象与正比例函数y=x的图象的一个交点为P.若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1),B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com