
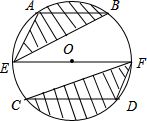
 如图,⊙O的直径EF为10cm,弦AB、CD分别为6cm、8cm,且AB∥EF∥CD.求图中阴影部分面积之和.
如图,⊙O的直径EF为10cm,弦AB、CD分别为6cm、8cm,且AB∥EF∥CD.求图中阴影部分面积之和. 分析 本题易得出△ABO与△ABE的面积相等,△OCD与△CDF的面积相等(这两组三角形都是同底等高),因此阴影部分的面积为扇形OAB的面积和扇形OCD的面积和.直接求两个扇形的面积由难度,因此可找出它们之间的关系再进行求解.过O作圆的直径MN,使得MN⊥EF与O,交AB于G;那么在Rt△BOG和Rt△COH中,易证得∠GBO=∠COH(通过两角的正弦值求证).因此可得出∠BOF=∠CON,即扇形OBF的面积与扇形OCN的面积相等,也就得出了扇形OBF与扇形OAE的面积和正好等于扇形OCD的面积;因此阴影部分的面积和正好是半个圆的面积,由此可得出所求的解.
解答 解:如图,作直径MN,使MN⊥EF于O,交AB于G,交CD于H;连接OA、OB、OC、OD;
在Rt△OBG中,BG=3cm,OB=5cm,因此OG=4cm;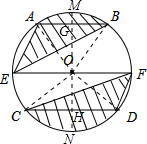
同理:在Rt△OCH中,CH=4cm,OC=5cm,因此OH=3cm;
sin∠DOF=$\frac{OH}{OD}$=$\frac{3}{5}$,
sin∠BOF=$\frac{OG}{OB}$=$\frac{4}{5}$,
sin∠COE=$\frac{OH}{OC}$=$\frac{3}{5}$,
sin∠AOE=$\frac{OG}{OA}$=$\frac{4}{5}$,
即∠DOF=∠AOM=∠COE=∠BOM,∠CON=∠DON=∠AOE=∠BOF,
因此S扇形OAE=S扇形OBF=S扇形CON=S扇形ODN
∴S阴影=S△ABE+S弓形AMB+S△CDF+S弓形CND
=S△OAB+S弓形AMB+S△OCD+S弓形CND
=S扇形OAB+S扇形OCN+S扇形ODN
=S扇形OAB+S扇形OAE+S扇形OBF
=$\frac{1}{2}$S⊙O
=12.5πcm2.
故图中阴影部分面积之和为12.5πcm2.
点评 本题考查扇形面积的计算,学生的观察能力及计算能力.本题中找出两个阴影部分面积之间的联系是解题的关系.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
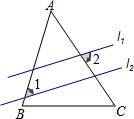 如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=55°,∠1=45°,则∠2的度数为( )| A. | 45° | B. | 55° | C. | 80° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
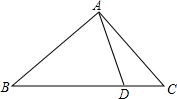 如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )
如图,D是△ABC一边BC上一点,连接AD,使△ABC∽△DBA的条件是( )| A. | AC:BC=AD:BD | B. | AC:BC=AB:AD | C. | AB2=CD•BC | D. | AB2=BD•BC |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
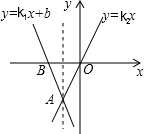 如图,直线y=k1x+b经过点A(-1,-2)和点B(-2,0),直线y=k2x经过点A,则二元一次方程组$\left\{\begin{array}{l}{y={k}_{1}x+b}\\{y={k}_{2}x}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,不等式k2x<k1x+b<0的解集为x<-1.
如图,直线y=k1x+b经过点A(-1,-2)和点B(-2,0),直线y=k2x经过点A,则二元一次方程组$\left\{\begin{array}{l}{y={k}_{1}x+b}\\{y={k}_{2}x}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,不等式k2x<k1x+b<0的解集为x<-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com