
【题目】 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
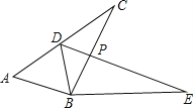
(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;
(2)求△DCP与△BPE的周长和.
【答案】(1)66°;(2)15.4
【解析】
(1)根据全等三角形的性质得到∠ABC=∠DBE,计算即可;
(2)根据全等三角形的性质求出BE、DE,根据三角形的周长公式计算即可.
解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AD+DC=4.8,BE=BC=4.1,
△DCP和△BPE的周长和=DC+DP+CP+BP+PE+BE=DC+DE+BC+BE=15.4.
故答案是:(1)66°;(2)15.4


科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y=![]() (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).

(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y=![]() (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
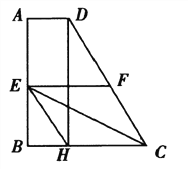
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:作点A关于直线l的对称点A'.
已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'. 点A'就是所求作的对称点.
由步骤①,得________
由步骤②,得________
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在真角坐标系中,矩形0ABC的顶点A,C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N.
(1)求直线DE的函数表达式和点M,N的坐标;
(2)若函数y=![]() (k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(3)求△OMN的面积S;
(4)若函教y=![]() (k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.
(k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(2m+3)x+m-1,
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴上的截距为-3,求m的值;
(3)若该函数的值y随自变量x的增大而减小,求m的取值范围;
(4)该函数图象不经过第二象限,求m的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com