
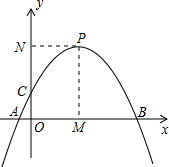
 ��ͼ���������µ�������y=a��x-2��2+k����x���ڵ�A��B����A�ڵ�B��ࣩ����y���������ڵ�C������ΪP��������P����x�ᣬy��Ĵ��ߣ�����ֱ�ΪM��N��
��ͼ���������µ�������y=a��x-2��2+k����x���ڵ�A��B����A�ڵ�B��ࣩ����y���������ڵ�C������ΪP��������P����x�ᣬy��Ĵ��ߣ�����ֱ�ΪM��N������ ��1���ȸ��������ߵĶԳ���ó�OM�ij��������ı���PMONΪ�����εó�k��ֵ����������ߵĶ������꣬����S��PCM=3���ɵó����ۣ�
��2����a=-1���������ߵĽ���ʽ���ٸ���CP=CM��PC=PM=k��MC=MP=k��������������ۣ�
��3������PM��y��ɵó���OCM=��PMC���ʿɵó�OC�ij������ɡ�CPM=45���֪��PCNΪ���������Σ���CN=PN=2��PM=ON=$\frac{9}{2}$��P��2��$\frac{9}{2}$�����ٰ�P��C��������������ֵ���ɣ�
��4������MQ�����MQD=��MPC=45�㣬�ʡ�MQB=135�㣮��BMΪб����x���·�������ֱ��������MEB�����Q����EΪԲ�ģ�MEΪ�뾶��Բ�ϣ�����PE������E�ڵ�Q����ʱPQ��С�����ɹ��ɶ������ɵó����ۣ�
��� �⣺��1���������ߵĽ���ʽΪy=a��x-2��2+k��
��OM=2��
��PMON������
��k=2��
�������ߵĶ�������Ϊ��2��k����S��PCM=3��
��$\frac{1}{2}$��2k=3�����k=3��
�ʴ�Ϊ��2��3��
��2��a=-1ʱ��y=��x-2��2+k=-x2+4x-4+k��
��C��0��-4+k����
������ã�P��2��k����M��2��0����
��CP=CMʱ��-4+k=$\frac{1}{2}$k�����k=8��
��PC=PM=kʱ��
��Et��PCN��
��PN=2��CN=k-��-4+k��=4��
��PC=k=$\sqrt{{PN}^{2}+{CN}^{2}}$=2$\sqrt{5}$��
��MC=MP=kʱ��
��Rt��OMC��
��OM=2��OC=-4+k��
��OC2+OM2=CM2��
�ࣨ-4+k��2+42=k2�����k=$\frac{5}{2}$����ȥ����
������������PCMΪ����������ʱ��k=8��2$\sqrt{5}$��
��3����PM��y�ᣬ
���OCM=��PMC��
��OC=$\frac{OM}{tan��CMP}$=$\frac{2}{\frac{4}{5}}$=$\frac{5}{2}$��
�ߡ�CPM=45�㣬
���PCN����������
��CN=PN=2��
��PM=ON=2+$\frac{5}{2}$=$\frac{9}{2}$��
��P��2��$\frac{9}{2}$����
��y=a��x-2��2+$\frac{9}{2}$��
��C��0��$\frac{5}{2}$������ã�4a+$\frac{9}{2}$=$\frac{5}{2}$�����a=-$\frac{1}{2}$��
��y=-$\frac{1}{2}$��x-2��2+$\frac{9}{2}$��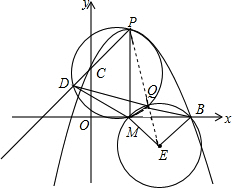
��4����ͼ������MQ�����MQD=��MPC=45�㣬
���MQB=135�㣮
��BMΪб����x���·�������ֱ��������MEB�����Q����EΪԲ�ģ�MEΪ�뾶��Բ�ϣ�����PE������E�ڵ�Q����ʱPQ��С��
��B��5��0����M��2��0����
��E��$\frac{7}{2}$��-$\frac{3}{2}$����
��ME=$\frac{3\sqrt{2}}{2}$��PE=$\sqrt{��\frac{3}{2}+\frac{9}{2}��^{2}+��\frac{3}{2}��^{2}}$=$\frac{3\sqrt{17}}{2}$��
��PQmin=$\frac{3\sqrt{17}}{2}$-$\frac{3\sqrt{2}}{2}$��
���� ���⿼����Ƕ��κ����ۺ��⣬�漰�����ɶ���������ǵ����Ǻ���ֵ�����������ε��ж������ʵ�֪ʶ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��֪Բ�� | B�� | ��֪�뾶 | C�� | ��ֱ֪�� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
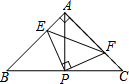 ��ͼ����Rt��ABC�У���BAC=90�㣬AB=AC��ֱ�ǡ�EPF�Ķ���P��BC���е㣬����EPF�ƶ���P��ת������PE��PF�ֱ�AB��AC�ڵ�E��F�������ĸ����ۣ�
��ͼ����Rt��ABC�У���BAC=90�㣬AB=AC��ֱ�ǡ�EPF�Ķ���P��BC���е㣬����EPF�ƶ���P��ת������PE��PF�ֱ�AB��AC�ڵ�E��F�������ĸ����ۣ�| A�� | �٢ڢ� | B�� | �ڢۢ� | C�� | �٢ۢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
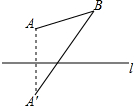 ��ͼ��A��B��ֱ��lͬ������㣬����A����ֱ��l�ĶԳƵ�A�䣬����A��B������A��B��ֱ��l�ľ���ֱ�Ϊ2��3�����߶�AB��A��B֮���������ϵ�ǣ�������
��ͼ��A��B��ֱ��lͬ������㣬����A����ֱ��l�ĶԳƵ�A�䣬����A��B������A��B��ֱ��l�ľ���ֱ�Ϊ2��3�����߶�AB��A��B֮���������ϵ�ǣ�������| A�� | A��B2-AB2=13 | B�� | A��B2-AB2=24 | C�� | A��B2+AB2=25 | D�� | A��B2+AB2=26 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
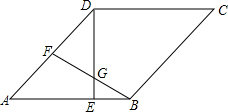 ��ͼ��������ABCD�У���A=60�㣬E��F�ֱ���AB��AD���е㣬DE��BF�ཻ�ڵ�G������CG��
��ͼ��������ABCD�У���A=60�㣬E��F�ֱ���AB��AD���е㣬DE��BF�ཻ�ڵ�G������CG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �����ܰɣ��ֵܣ�����Ŀ�飬Ԥ���һ���µ���Ϸ�������ܡ�·���辭A��B��C��D�ĵأ���ͼ������A��B��C������ͬһֱ���ϣ�D����A�ر�ƫ��30�㷽����C�ر�ƫ��45�㷽��C����A�ر�ƫ��75�㷽����BC=CD=20m��
�����ܰɣ��ֵܣ�����Ŀ�飬Ԥ���һ���µ���Ϸ�������ܡ�·���辭A��B��C��D�ĵأ���ͼ������A��B��C������ͬһֱ���ϣ�D����A�ر�ƫ��30�㷽����C�ر�ƫ��45�㷽��C����A�ر�ƫ��75�㷽����BC=CD=20m���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com