
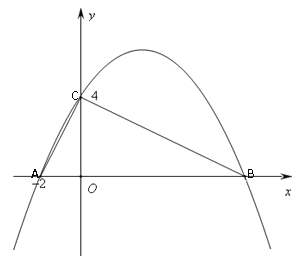
【题目】如图,在平面直角坐标系中,抛物线![]() 经过Rt△ABC的三个顶点,其中∠ACB=90°,点A坐标为(-2,0),点C坐标为(0,4).
经过Rt△ABC的三个顶点,其中∠ACB=90°,点A坐标为(-2,0),点C坐标为(0,4).
(1)求该抛物线的解析式.
(2)如果将线段OB绕原点O逆时针旋转60°到0D位置,那么点B的对应点D是否会落在该抛物线的对称轴上?请说明理由.
【答案】(1)![]() ;(2)点D不会落在该抛物线的对称轴上.理由见解析.
;(2)点D不会落在该抛物线的对称轴上.理由见解析.
【解析】试题分析:(1)首先证明△ACO∽△CBO,根据相似三角形的性质可得![]() ,然后可得B点坐标,再利用待定系数法求出抛物线解析式即可;
,然后可得B点坐标,再利用待定系数法求出抛物线解析式即可;
(2)根据抛物线解析式计算出对称轴,再根据等边三角形的判定可得△BOD是等边三角形,再根据等腰三角形三线合一的性质可得D点横坐标,进而可得答案.
试题解析:(1)由题意得:CO⊥AB,OA=2,OC=4
∵∠ACB=90°, CO⊥AB
∴∠ACO+∠BCO=90°,∠ACO+∠CAO=90°,∠AOC=∠COB=90°
∴∠BCO=∠CAO
∴△AOC∽△COB
∴![]()
∴![]() 解得 OB=8
解得 OB=8
∴点B坐标为(8,0)分
∵抛物线![]() 经过点A、B、C
经过点A、B、C
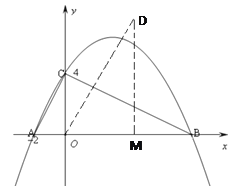
∴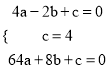
解得
∴该抛物线的解析式为![]() .
.
(2)点D不会落在该抛物线的对称轴上.
理由:作DM⊥x轴于点M,则在Rt△ODM中,OD=OB=8,∠DOM=60°
∴∠ODM=30°
∴OM=![]() .
.
∴点D的横坐标为4
又由(1)可知,该抛物线的对称轴是直线x=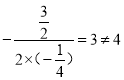
∴旋转后点B的对应点D不会落在该抛物线的对称轴上.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】某校举办初中生演讲比赛,每班派一名学生参赛,现某班有A,B,C三名学生竞选,他们的笔试成绩和口试成绩分别用两种方式进行了统计,如表和图1:


(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本年级段的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按3:4:3的比例确定最后成绩,请计算这三名学生的最后成绩,并根据最后成绩判断谁能当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店从厂家以每件21元的价格购进一批商品,该商品可以自行定价,且每件商品售价与其销售量是一次函数关系。若每件商品售价为25元,则可卖出100件;若每件商品售价为30元,则可卖出50件,但物价局限定每件商品加价不能超过进价的20%
(1)求该商品的销售量与售价的函数关系式;
(2)若商店计划要赚400元,需要卖出多少件商品?每件商品应售价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(﹣5,1)、(﹣1,4),结合所给的平面直角坐标系解答下列问题: 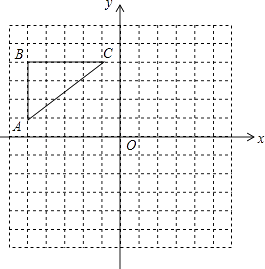
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)点C1的坐标是;点C2的坐标是;△ABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中,装有除颜色外其余均相同的红、蓝两种球,已知其中红球有3个,且从中任意摸出一个是红球的概率为0.75.
(1)根据题意,袋中有 个蓝球.
(2)若第一次随机摸出一球,不放回,再随机摸出第二个球.请用画树状图或列表法求“摸到两球中至少一个球为蓝球(记为事件A)”的概率P(A).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)27﹣19+(﹣7)﹣32;
(2)(﹣7)÷(﹣ ![]() )×(﹣
)×(﹣ ![]() );
);
(3)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣36)
)×(﹣36)
(4)﹣14﹣ ![]() ×[2﹣(﹣3)2].
×[2﹣(﹣3)2].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com