
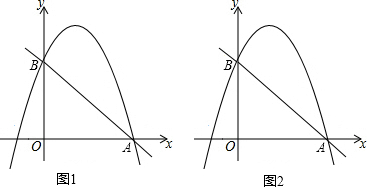
���� ��1�������A��B�������꣬���ô���ϵ���������Գ��ṫʽ�з����������⣮
��2����ͼ1�У���P��m��-$\frac{2}{3}$m2+$\frac{4}{3}$m+2������PQ��y�ύAB��Q����Q��m��-$\frac{2}{3}$m+2�����������κ��������ö��κ��������ʽ�����⣮
��3��������������ͼ2�У�����N�ڶԳ�����ʱ����AG��OA��PG��AG��G��NH��AG��H������ͼ3�У�����M�ڶԳ�����ʱ����PG�ͶԳ�����G��AH��PG��H���ֱ�����ȫ�������ε����ʣ��г����̽�����⣮
��� �⣺��1����y=-$\frac{2}{3}$x+2����x=0��y=2����y=0��x=3��
��B��0��2����A��3��0����
������$\left\{\begin{array}{l}{c=2}\\{9a+3b+c=0}\\{-\frac{b}{2a}=1}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{4}{3}}\\{c=2}\end{array}\right.$��
�������ߵĽ���ʽΪy=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2��
��2����ͼ1�У���P��m��-$\frac{2}{3}$m2+$\frac{4}{3}$m+2������PQ��y�ύAB��Q����Q��m��-$\frac{2}{3}$m+2����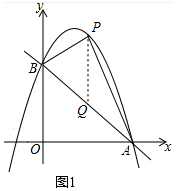
��S��PAB=$\frac{1}{2}$•��-$\frac{2}{3}$m2+$\frac{4}{3}$m+2+$\frac{2}{3}$m-2��•3=-m2+3m=-��m-$\frac{3}{2}$��2+$\frac{9}{4}$��
��-1��0��
��m=$\frac{3}{2}$ʱ����PAB������ʱP��$\frac{3}{2}$��$\frac{5}{2}$����
��3������ͼ2�У�����N�ڶԳ�����ʱ����AG��OA��PG��AG��G��NH��AG��H��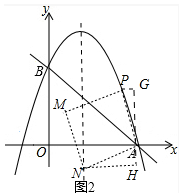
��PA=AN����G=��H=90�㣬��PAG=��ANH��
���APG�ա�NAH��
��AG=NH=2��
��y=2ʱ��-$\frac{2}{3}$x2+$\frac{4}{3}$x+2=2�����x=2��0����������
���ʱP��2��2����
����ͼ3�У�����M�ڶԳ�����ʱ����PG�ͶԳ�����G��AH��PG��H��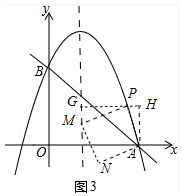
�ɡ�PAH�ա�MPG����AH=PG����P��m��-$\frac{3}{2}$m2+$\frac{4}{3}$m+2����
����m-1=-$\frac{3}{2}$m2+$\frac{4}{3}$m+2�����m=$\frac{1+\sqrt{163}}{9}$��$\frac{1-\sqrt{163}}{9}$����������
��ʱ��P���꣨$\frac{1+\sqrt{163}}{9}$��$\frac{\sqrt{163}-8}{9}$����
��������������P����Ϊ��2��2����$\frac{1+\sqrt{163}}{9}$��$\frac{\sqrt{163}-8}{9}$��ʱ����APΪ����������APMN��������M��Nǡ�����������߶Գ����ϣ�
���� ���⿼���˶��κ������ۺ����á�ȫ�������ε��ж������ʡ������ε��ж������ʡ�����Ĺؼ����������մ���ϵ����ȷ����������ʽ��ѧ�ṹ�����κ��������ֵ���⣬ѧ�����ӳ��ø����߹���ȫ�������ν�����⣬�����п�ѹ���⣮


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABD����AEC���ǵȱ������Σ���CD��BE�ཻ�ڵ�O����֤��
��ͼ����ABD����AEC���ǵȱ������Σ���CD��BE�ཻ�ڵ�O����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ı���ABCD�У���A=60�㣬AD=2��AB=3����M��N�ֱ�Ϊ�߶�BC��AB�ϵĶ��㣨���˵㣬����M�����B�غϣ�����E��F�ֱ�ΪDM��MN���е㣬��EF���ȵ����ֵΪ��������
��ͼ���ı���ABCD�У���A=60�㣬AD=2��AB=3����M��N�ֱ�Ϊ�߶�BC��AB�ϵĶ��㣨���˵㣬����M�����B�غϣ�����E��F�ֱ�ΪDM��MN���е㣬��EF���ȵ����ֵΪ��������| A�� | $\frac{\sqrt{7}}{2}$ | B�� | $\sqrt{7}$ | C�� | $\sqrt{3}$ | D�� | $\frac{\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��D�ǵ���ֱ��������ABCб��BC��һ�㣨�����B�غϣ�����AD���߶�AD�Ƶ�A��ʱ�뷽����ת90��õ��߶�AE����CE����֤��BD��CE��
��ͼ����֪��D�ǵ���ֱ��������ABCб��BC��һ�㣨�����B�غϣ�����AD���߶�AD�Ƶ�A��ʱ�뷽����ת90��õ��߶�AE����CE����֤��BD��CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com