
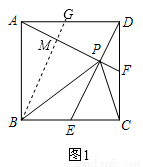
如图,正方形ABCD中,E、F均为中点,则下列结论中:①AF⊥DE; ②AD=BP; ③PE+PF=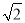 PC; ④PE+PF=PC。其中正确的是( )
PC; ④PE+PF=PC。其中正确的是( )
A.①④ B.①②④ C.①③ D.①②③
D.
【解析】
试题分析:如题图,
∵正方形ABCD,E,F均为中点,∴AD=DC=BC,∠ADC=∠DCB,EC=DF=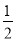 DC.
DC.
∵在△ADF和△DCE中,AD=DC,∠ADF=∠DCE,DF=CE,∴△ADF≌△DCE(SAS).∴∠AFD=∠DEC.
∵∠DEC+∠CDE=90°,∴∠AFD+∠CDE=90°=∠DPF
∴AF⊥DE.∴①正确.
如图1,过B作BG∥DE交AD于G,交AP于M,
∵AF⊥DE,BG∥DE,E是BC中点,∴BG⊥AP,G是AD的中点.∴BG是AP的垂直平分线.
∴△ABP是等腰三角形.∴BP=AB=AD,∴②正确.
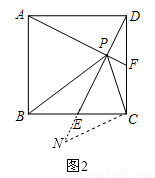
如图2,延长DE至N,使得EN=PF,连接CN,
∵∠AFD=∠DEC ,∴∠CEN=∠CFP.
又∵E,F分别是BC,DC的中点,∴CE=CF,
∵在△CEN和△CFP中,CE=CF,∠CEN=∠CFP,EN=PF,∴△CEN≌△CFP(SAS).∴CN=CP,∠ECN=∠PCF.
∵∠PCF+∠BCP=90°,∴∠ECN+∠BCP=∠NCP=90°.
∴△NCP是等腰直角三角形.∴PN=PE+NE=PE+PF=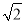 PC.∴③正确,④错误.
PC.∴③正确,④错误.
∴①②③正确.
故选D.
考点:1.正方形的性质;2.全等三角形的性质和判定;3.线段垂直平分线性质;4.等腰三角形的性质和判定;5.垂直定义.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源:2016届北京市七年级下学期期末数学试卷(解析版) 题型:选择题
若点P(1-m,2m-4)在第四象限内,则m的取值范围是( )
A.m<1 B.1<m<2 C.m<2 D.m>2
查看答案和解析>>
科目:初中数学 来源:2015届重庆市合川区第五学区八年级下学期半期考试数学试卷(解析版) 题型:解答题
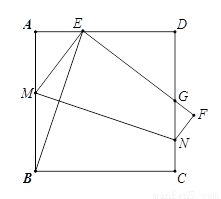
如图,M、N是正方形ABCD边AB、CD上两动点,连接MN,将四边形BCNM沿MN折叠,使点B落在AD边上点E处、点C落在点F.
(1)求证:BE平分∠AEF;
(2)求证:C△EDG=2AB(注:C△EDG表示△EDG的周长)
查看答案和解析>>
科目:初中数学 来源:2015届重庆市合川区第五学区八年级下学期半期考试数学试卷(解析版) 题型:填空题
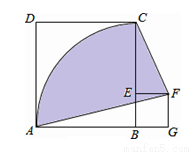
如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画圆,连结AF,CF,则图中阴影部分面积为 .
查看答案和解析>>
科目:初中数学 来源:2015届重庆市合川区第五学区八年级下学期半期考试数学试卷(解析版) 题型:选择题
如图,有两颗树,一颗高10米,另一颗高4米,两树相距8米.一只鸟从一颗树的树梢飞到另一颗树的树梢,问小鸟至少飞行( )

A.8米 B.10米 C.12米 D.14米
查看答案和解析>>
科目:初中数学 来源:2015届重庆市八年级下期期末考试数学试卷(解析版) 题型:解答题
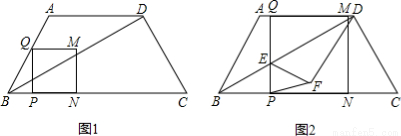
如图1,梯形ABCD中,AD∥BC,AB=AD=DC=5,BC=11.一个动点P从点B出发,以每秒1个单位长度的速度沿线段BC方向运动,过点P作PQ⊥BC,交折线段BA-AD于点Q,以PQ为边向右作正方形PQMN,点N在射线BC上,当Q点到达D点时,运动结束.设点P的运动时间为t秒(t>0).
(1)当正方形PQMN的边MN恰好经过点D时,求运动时间t的值;
(2)在整个运动过程中,设正方形PQMN与△BCD的重合部分面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,当点Q在线段AD上运动时,线段PQ与对角线BD交于点E,将△DEQ沿BD翻折,得到△DEF,连接PF.是否存在这样的t,使△PEF是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2015届重庆市八年级下期期末考试数学试卷(解析版) 题型:选择题
已知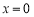 是关于的一元二次方程
是关于的一元二次方程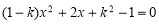 的根,则常数的值为( )
的根,则常数的值为( )
A.0或1 B.1 C.-1 D.1或-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com