
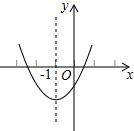 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc<0;②2a+b=0;③a+b+c>0;④b2>4ac.其中正确的有①③④.
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①abc<0;②2a+b=0;③a+b+c>0;④b2>4ac.其中正确的有①③④. 分析 ①首先根据抛物线开口向上,可得a>0;然后根据对称轴在y轴左边,可得b>0;最后根据抛物线与y轴的交点在x轴的下方,可得c<0,据此判断出abc<0即可;
②根据对称轴为x=-1,得出-$\frac{b}{2a}$=-1进行判断即可;
③把x=1代入解析式后根据图象判断即可;
④根据与x轴有两个交点即可判断b2-4ac>0.
解答 解:①因为抛物线开口向上,所以a>0;
因为对称轴在y轴左边,所以b>0;
因为抛物线与y轴的交点在x轴的下方,所以c<0;
可得abc<0,正确;
②因为对称轴为x=-1,可得:-$\frac{b}{2a}$=-1,
b=2a,所以2a+b=0是错误的;
③把x=1代入解析式,y=a+b+c,由图象得出此时y>0,
所以a+b+c>0,正确;
④因为图象与x轴有两个交点,可得:b2-4ac>0,
即b2>4ac,正确.
故答案为:①③④.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
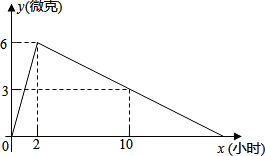 某医药研究所研发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达每毫升6微克,接着逐步衰减,服药后10小时血液中含药量为3微克,含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.
某医药研究所研发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时血液中含药量最高,达每毫升6微克,接着逐步衰减,服药后10小时血液中含药量为3微克,含药量y(微克)随时间x(小时)的变化如图所示,当成人按规定剂量服药后.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com