
����Ŀ���ڡ��IJ��ᡱ�ڼ䣬ij��˾չ����ͼ��ʾ�ij����ι���Ʒ���ù���Ʒ��60cm����40cm���м����п�����ͬ������˿�ߣ� 
��1����˿�ߵ����Ϊ650cm2 �� ��˿�ߵĿ��ȣ�
��2����֪�ù���Ʒ�ijɱ���40Ԫ/��������Ե���100Ԫ/�����ۣ���ôÿ����۳�200������ÿ������֧���ĸ��ַ���2000Ԫ���������۾��飬��������۵��۽���1Ԫ��ÿ��ɶ��۳�20����ͬʱ��Ϊ������������ù�˾ÿ������Ҫ����800������ô�ù�˾Ӧ�ð����۵��۶�Ϊ����Ԫ������ʹÿ�������������������������Ƕ��٣�
���𰸡�
��1���⣺�軨�ߵĿ���Ϊxcm����������ã�
��60��2x����40��x��=60��40��650��
��ã�x=5��x=65����ȥ����
��˿�ߵĿ���Ϊ5cm
��2���⣺��ÿ������Ʒ����xԪ���ۣ�����yԪ�����������ɵã�
y=��x��40��[200+20��100��x��]��2000=��20��x��75��2+22500��
�����ۼ�������Ϊ800������40��x��70
�൱x=70ʱ�������ֵ��y=22000
���ۼ�Ϊ70Ԫʱ���������22000Ԫ
����������1��������ߵĿ���Ȼ���ʾ�����ߵij������������ʽ��ʾ������������г�������⣻��2���ȸ���������ÿ������Ʒ����ΪxԪ���ۣ�����yԪ����xԪ����������ܼ���Ϊ��200+20x����ÿ����õ�����Ϊ��100��x��40������ʱ���ݻ�õ�����=�������ܼ�����ÿ������Ʒ��õ������г����η��̣��ٸ�������κ�����ֵ�ķ���������õ�������ɣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������⣺��ͼ1��P,Q�DZ�������400m�ܵ������㣬���ܵ���P��Q�ȿ�����ʱ�룬Ҳ����˳ʱ�룬���ǰ����ܵ��ӵ�P����Q��˳ʱ��·������ʱ��·�̵Ľ�С�߽�P��Q�������ѻ�����.(��ͼ1��PQ˳ʱ���·��Ϊ120m,��ʱ���·��Ϊ280m,��PQ����ѻ�����Ϊ120m).
���������һ��У�˶�800mԤ�����У���ͼ2�мס��������˶�Ա����ͬʱͬ�شӵ�M�������������ܲ�������֮�����ѻ�����y(m)�����õ�ʱ��x(s)֮��ĺ�����ϵ��ͼ��ʾ������������⣺
��1��a=_________,�ҵ��ٶ�Ϊ___________.
��2�����߶�BC�Ľ���ʽ����д���Ա����ķ�Χ.
��3���������˶�����1000mԤ����������ɱ������Ƿ��п��ܱ��Ҷ���һȦ������˵��.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=x��ͼ��Ϊֱ��l��
��1���۲���̽��
��֪��A��A������B��B���ֱ����ֱ��l�Գƣ���λ�ú�������ͼ��ʾ������ͼ�б��C��4����1��������l�ĶԳƵ�C����λ�ã���д��C��������_____��
��2�������뷢��
�۲���������ԳƵ�����꣬��ᷢ�֣�
ƽ��ֱ������ϵ�е�P��a��b������ֱ��l�ĶԳƵ�P��������Ϊ_____��
��3����������չ
��֪����M����3��3����N����4����1��������ֱ��l��������Q��ʹ��Q��M��N����ľ���֮����С���������Ӧ����Сֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������ֱ�ΪA��1��1����B��4��2����C��3��4���� 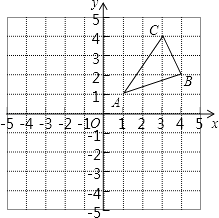
��1�����뻭����ABC����ƽ��5����λ���Ⱥ�õ��ġ�A1B1C1��
���뻭����ABC����ԭ��ԳƵġ�A2B2C2��
��2����x��������һ��P��ʹ��PAB���ܳ���С���뻭����PAB����ֱ��д��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У���ACBΪ��ǣ���DΪ����BC��һ�㣬����AD����ADΪһ������AD���Ҳ���������ADEF������ʾ�������ε������߶���ȣ��ĸ��Ƕ���ֱ�ǣ�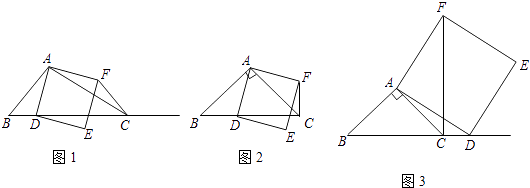
��1�����AB=AC����BAC=90�㣬
�ٵ���D���߶�BC��ʱ�����B���غϣ�����ͼ2���߶�CF��BD����ֱ�ߵ�λ�ù�ϵΪ �� �߶�CF��BD��������ϵΪ��
�ڵ���D���߶�BC���ӳ�����ʱ����ͼ3�����еĽ����Ƿ���Ȼ��������˵�����ɣ�
��2�����AB��AC����BAC����ǣ���D���߶�BC�ϣ�����ACB��������ʱ��CF��BC����C��F���غϣ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����BAC=54������BAC��ƽ������AB�Ĵ�ֱƽ���߽��ڵ�O������C��EF��E��BC�ϣ�F��AC�ϣ��۵�����C���Oǡ���غϣ�����OEC= �ȣ�
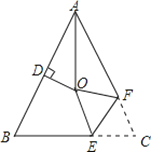
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ�ȱ������Σ�AE=CD��AD��BE�ཻ�ڵ�P��BQ��AD��Q��
(1����֤����ADC�ա�BEA��
��2����PQ=4��PE=1����AD�ij���
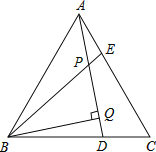
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱ�������ABC�ı߳�Ϊ12����PΪAC��һ�㣬��D��CB���ӳ����ϣ���BD=AP������PD��AB�ڵ�E��PE��AB�ڵ�F�����߶�EF�ij�Ϊ��������

A. 6 B. 5
C. 4.5 D. ��AP�ij����й�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������8�֣�
��һ�����������У�һ��������һ������Ӽ������ҵأ������ҵ�ж���أ��������Ӽس���![]() ��h��ʱ��������صľ���Ϊ
��h��ʱ��������صľ���Ϊ![]() ��km����
��km����![]() ��
��![]() �ĺ�����ϵ��ͼ��ʾ��
�ĺ�����ϵ��ͼ��ʾ��
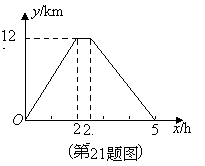
����ͼ����Ϣ������������⣺
��1�������������������ٶ��Ƿ���ͬ����˵�����ɣ�
��2������![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��3�������������Ӽس���4hʱ��صľ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com