
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:其中,正确的个数有( )
①b2﹣4ac<0;②a﹣b+c<0;③abc>0;④m>﹣2.
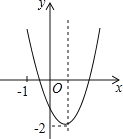
A.1B.2C.3D.4
科目:初中数学 来源: 题型:
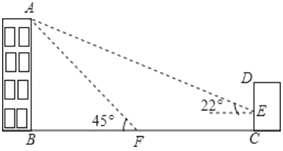
【题目】如图,某办公楼![]() 的后面有一建筑物
的后面有一建筑物![]() ,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子
,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子![]() ,而当光线与地面夹角是45°时,办公楼顶
,而当光线与地面夹角是45°时,办公楼顶![]() 在地面上的影子
在地面上的影子![]() 与墙角
与墙角![]() 有25米的距离(
有25米的距离(![]() 在一条直线上).
在一条直线上).
(1)求办公楼![]() 的高度;
的高度;
(2)若要在![]() ,
,![]() 之间挂一些彩旗,请你求出
之间挂一些彩旗,请你求出![]() ,
,![]() 之间的距离.(参考数据:
之间的距离.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
七年级 | a | 85 | b | S七年级2 |
八年级 | 85 | c | 100 | 160 |
(1)根据图示填空:a= ,b= ,c= ;
(2)结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?
(3)计算七年级代表队决赛成绩的方差S七年级2,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为表彰在“了不起我的国”演讲比赛中获奖的选手,决定购买甲、乙两种图书作为奖品.已知购买30本甲种图书,50本乙种图书共需1350元;购买50本甲种图书,30本乙种图书共需1450元.
(1)求甲、乙两种图书的单价分别是多少元?
(2)学校要求购买甲、乙两种图书共40本,且甲种图书的数量不少于乙种图书数量的![]() ,请设计最省钱的购书方案.
,请设计最省钱的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
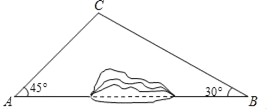
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
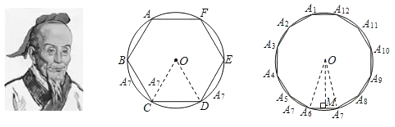
【题目】我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率![]() .刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为
.刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为![]() ,圆内接正六边形的周长
,圆内接正六边形的周长![]() ,计算
,计算![]() ;圆内接正十二边形的周长
;圆内接正十二边形的周长![]() ,计算
,计算![]() ;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率
;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率![]() __________.(参考数据:
__________.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com