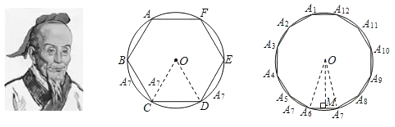
【题目】我国魏晋时期的数学家刘徽（263年左右）首创“割圆术”，所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率，刘徽计算出圆周率
．刘微从正六边形开始分割圆，每次边数成倍增加，依次可得圆内接正十二边形，圆内接正二十四边形，…，割得越细，正多边形就越接近圆．设圆的半径为
，圆内接正六边形的周长
，计算
；圆内接正十二边形的周长
，计算
；那么分割到圆内接正二十四边形后，通过计算可以得到圆周率
__________．（参考数据：
，
）
科目：初中数学 来源： 题型：
【题目】某超市销售一种商品，成本价为50元/千克，规定每千克售价不低于成本价，且不高于85元．经过市场调查，该商品每天的销售量
（千克）与售价
（元/千克）满足一次函数关系，部分数据如下表：
售价 | 50 | 60 | 70 |
销售量 | 120 | 100 | 80 |
（1）求与之间的函数表达式．
（2）设该商品每天的总利润为
（元），则当售价定为多少元/千克时，超市每天能获得最大利润？最大利润是多少元？
（3）如果超市要获得每天不低于1600元的利润，且符合超市自己的规定，那么该商品的售价的取值范围是多少？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】记某商品销售单价为x元，商家销售此种商品每月获得的销售利润为y元，且y是关于x的二次函数．已知当商家将此种商品销售单价分别定为55元或75元时，他每月均可获得销售利润1800元；当商家将此种商品销售单价定为80元时，他每月可获得销售利润1550元，则y与x的函数关系式是（ ）
A.y＝﹣（x﹣60）2+1825B.y＝﹣2（x﹣60）2+1850
C.y＝﹣（x﹣65）2+1900D.y＝﹣2（x﹣65）2+2000
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，并且关于x的一元二次方程ax2+bx+c﹣m＝0有两个不相等的实数根，下列结论：其中，正确的个数有（ ）
①b2﹣4ac＜0；②a﹣b+c＜0；③abc＞0；④m＞﹣2．
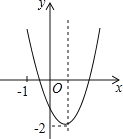
A.1B.2C.3D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
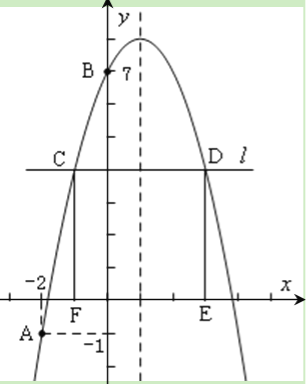
【题目】（11·永州）（本题满分10分）如图，已知二次函数
的图象经过
A（
，
），B（0,7）两点．
⑴ 求该抛物线的解析式及对称轴；
⑵ 当
为何值时，
？
⑶ 在
轴上方作平行于
轴的直线
，与抛物线交于C，D两点（点C在对称轴的左侧），
过点C，D作
轴的垂线，垂足分别为F，E．当矩形CDEF为正方形时，求C点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】新华加工厂生产某种零件，该厂为了鼓励销售代理订货，提供了如下信息：
①每个零件的成本价为40元；②若一次订购该零件100个以内，出厂价为60元，若订购量超过100个时，每多订1个，订购的全部零件的出厂单价就降低0.02元；③实际出厂单价不能低于51元．根据以上信息，解答下列问题：
（1）当一次订购量达到 个时，零件的实际出厂单价降为51元；
（2）设一次订购量为
个，零件的实际出厂单价为
元，求与的函数表达式；
（3）如果销售代理一次订购500个零件，该厂的利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
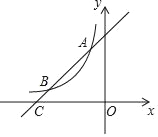
【题目】如图，一次函数y=x+4的图象与反比例函数y=
（k为常数且k≠0）的图象交于A（﹣1，a），B两点，与x轴交于点C．
（1）求此反比例函数的表达式；
（2）若点P在x轴上，且S△ACP=
S△BOC，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店购进
、
两种商品，购买1个商品比购买1个商品多花10元，并且花费300元购买商品和花费100元购买商品的数量相等．
（1）求购买一个商品和一个商品各需要多少元；
（2）商店准备购买、两种商品共80个，若商品的数量不少于商品数量的4倍，并且购买、商品的总费用不低于1000元且不高于1050元，那么商店有哪几种购买方案？
查看答案和解析>>
科目：初中数学 来源： 题型：
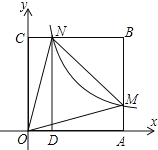
【题目】如图，在平面直角坐标系中，正方形OABC的顶点O与原点重合，顶点A，C分别在x轴、y轴上，反比例函数
(k≠0，x>0)的图象与正方形的两边AB、BC分别交于点M、N，连接OM、ON、MN．若∠MON=45°，MN=2，则k的值为_______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
