
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
【答案】(1)购买一个![]() 商品需要15元,购买一个
商品需要15元,购买一个![]() 商品需要5元;(2)商店有2种购买方案,方案①:购进
商品需要5元;(2)商店有2种购买方案,方案①:购进![]() 商品65个、
商品65个、![]() 商品15个;方案②:购进
商品15个;方案②:购进![]() 商品64个、
商品64个、![]() 商品16个.
商品16个.
【解析】
(1)设购买一个![]() 商品需要
商品需要![]() 元,则购买一个
元,则购买一个![]() 商品需要
商品需要![]() 元,根据数量=总价÷单价结合花费300元购买
元,根据数量=总价÷单价结合花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等,即可得出关于
商品的数量相等,即可得出关于![]() 的分式方程,解之经检验后即可得出结论;
的分式方程,解之经检验后即可得出结论;
(2)设购买![]() 商品
商品![]() 个,则购买
个,则购买![]() 商品
商品![]() 个,根据
个,根据![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍并且购买
商品数量的4倍并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,即可得出关于
商品的总费用不低于1000元且不高于1050元,即可得出关于![]() 的一元一次不等式组,解之即可得出
的一元一次不等式组,解之即可得出![]() 的取值范围,再结合
的取值范围,再结合![]() 为整数即可找出各购买方案.
为整数即可找出各购买方案.
解:(1)设购买一个![]() 商品需要
商品需要![]() 元,则购买一个
元,则购买一个![]() 商品需要
商品需要![]() 元,
元,
依题意,得:![]() ,
,
解得:![]() ,
,
经检验,![]() 是原方程的解,且符合题意,
是原方程的解,且符合题意,
∴![]() .
.
答:购买一个![]() 商品需要15元,购买一个
商品需要15元,购买一个![]() 商品需要5元.
商品需要5元.
(2) 设购买![]() 商品
商品![]() 个,则购买
个,则购买![]() 商品
商品![]() 个,
个,
依题意,得: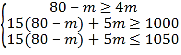 ,
,
解得:![]() .
.
∵![]() 为整数,
为整数,
∴![]() 或16.
或16.
∴商店有2种购买方案,方案①:购进![]() 商品65个、
商品65个、![]() 商品15个;方案②:购进
商品15个;方案②:购进![]() 商品64个、
商品64个、![]() 商品16个.
商品16个.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
七年级 | a | 85 | b | S七年级2 |
八年级 | 85 | c | 100 | 160 |
(1)根据图示填空:a= ,b= ,c= ;
(2)结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?
(3)计算七年级代表队决赛成绩的方差S七年级2,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
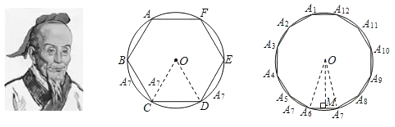
【题目】我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率![]() .刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为
.刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为![]() ,圆内接正六边形的周长
,圆内接正六边形的周长![]() ,计算
,计算![]() ;圆内接正十二边形的周长
;圆内接正十二边形的周长![]() ,计算
,计算![]() ;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率
;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率![]() __________.(参考数据:
__________.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题:
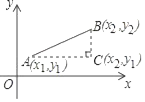
如图,为了求平面直角坐标系中任意两点A(x1,y1)、B(x2,y2)之间的距离,可以AB为斜边作Rt△ABC,则点C的坐标为C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,根据勾股定理可得AB=![]() ,反之,可以将代数式
,反之,可以将代数式![]() 的值看做平面内点(x1,y1)到点(x2,y2)的距离.
的值看做平面内点(x1,y1)到点(x2,y2)的距离.
例如∵![]() =
=![]() =
=![]() ,可将代数式
,可将代数式![]() 看作平面内点(x,y)到点(﹣1,3)的距离
看作平面内点(x,y)到点(﹣1,3)的距离
根据以上材料解决下列问题
(1)求平面内点M(2,﹣3)与点N(﹣1,3)之间的距离;
(2)求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
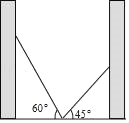
【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左侧墙上与地面成60°角时,梯子顶端距离地面2![]() 米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).
米,若保持梯子底端位置不动,将梯子斜靠在右端时,与地面成45°,则小巷的宽度为_____米(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
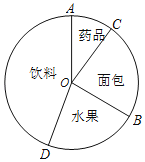
【题目】参加学校运动会,八年级1班第一天购买了水果,面包,饮料,药品等四种食品,四种食品购买金额的统计图表如图所示,若将水果、面包、药品三种食品统称为非饮料食品,并规定t=![]() .
.
(1)①求t的值;![]()
②求扇形统计图中钝角∠AOB的度数.
(2)根据实际需要,该班第二天购买这四种食品时,增加购买饮料金额,同时减少购买面包金额,假设增加购买饮料金额的25%等于减少购买面包的金额,且购买面包的金额不少于100元,求t的取值范围.
金额 食品 | 金额(单位:元) |
水果 | 100 |
面包 | 125 |
饮料 | 225 |
药品 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com