
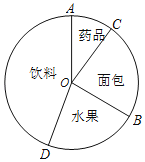
����Ŀ���μ�ѧУ�˶��ᣬ���꼶1���һ�칺����ˮ������������ϣ�ҩƷ������ʳƷ������ʳƷ�������ͳ��ͼ����ͼ��ʾ������ˮ���������ҩƷ����ʳƷͳ��Ϊ������ʳƷ�����涨t��![]() ��
��
��1������t��ֵ��![]()
��������ͳ��ͼ�ж۽ǡ�AOB�Ķ�����
��2������ʵ����Ҫ���ð�ڶ��칺��������ʳƷʱ�����ӹ������Ͻ�ͬʱ���ٹ���������������ӹ������Ͻ���25%���ڼ��ٹ�������Ľ��ҹ�������Ľ�����100Ԫ����t��ȡֵ��Χ��
��� ʳƷ | ����λ��Ԫ�� |
ˮ�� | 100 |
��� | 125 |
���� | 225 |
ҩƷ | 50 |
���𰸡���1���� ![]() ���� 126�㣻��2��
���� 126�㣻��2��![]() ��t��
��t��![]()
��������
��1���ٸ����������Ŀ�е����ݿ��Լ����t��ֵ��
�ڸ���ͳ�Ʊ��е����ݿ��Լ��������ͳ��ͼ�ж۽ǡ�AOB�Ķ�����
��2���������⣬�����г�����t�IJ���ʽ���Ӷ��������t��ȡֵ��Χ��
�⣺��1����������ɵã�
t��![]() ��
��![]() ��
��![]() ��
��
������ͳ��ͼ�ж۽ǡ�AOB�Ķ���Ϊ��360���![]() ��360���
��360���![]() ��126�㣻
��126�㣻
��2������ٹ�������Ľ��ΪxԪ�������ӹ������ϵĽ��Ϊ4xԪ��
t��![]() ��
��![]() ��
��
��x��![]() ��
��
��125��x��100��
��x��25��
��![]() ��25��
��25��
��ã�t��![]() ��
��
�ɣ�1������֪����ԭ���Ĺ������ʱt��![]() ��
��
��t�� ȡֵ��Χ��![]() ��t��
��t��![]() ��
��


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��![]() ��
��![]() ������Ʒ������1��
������Ʒ������1��![]() ��Ʒ�ȹ���1��
��Ʒ�ȹ���1��![]() ��Ʒ�10Ԫ�����һ���300Ԫ����
��Ʒ�10Ԫ�����һ���300Ԫ����![]() ��Ʒ�ͻ���100Ԫ����
��Ʒ�ͻ���100Ԫ����![]() ��Ʒ��������ȣ�
��Ʒ��������ȣ�
��1������һ��![]() ��Ʒ��һ��
��Ʒ��һ��![]() ��Ʒ����Ҫ����Ԫ��
��Ʒ����Ҫ����Ԫ��
��2���̵�������![]() ��
��![]() ������Ʒ��80������
������Ʒ��80������![]() ��Ʒ������������
��Ʒ������������![]() ��Ʒ������4�������ҹ���
��Ʒ������4�������ҹ���![]() ��
��![]() ��Ʒ���ܷ��ò�����1000Ԫ�Ҳ�����1050Ԫ����ô�̵����ļ��ֹ�����
��Ʒ���ܷ��ò�����1000Ԫ�Ҳ�����1050Ԫ����ô�̵����ļ��ֹ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
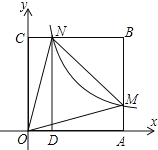
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O��ԭ���غϣ�����A��C�ֱ���x�ᡢy���ϣ�����������![]() (k��0��x>0)��ͼ���������ε�����AB��BC�ֱ��ڵ�M��N������OM��ON��MN������MON=45����MN=2����k��ֵΪ_______��
(k��0��x>0)��ͼ���������ε�����AB��BC�ֱ��ڵ�M��N������OM��ON��MN������MON=45����MN=2����k��ֵΪ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��������������x���Ͼ���������ͬ�㣬��ô���dz��������������ǡ�ͬ���������ߡ�����x���Ͼ�����������ͬ���Ϊ��ͬ���㡱����֪������y=x2+bx+c����(��2��0)��(��4��0)����һ�������ǡ�ͬ���������ߡ���������y=ax2+ex+f������(��3��3)��
��1����b��c��a��ֵ��
��2����֪������y=��x2+2x+3��������yn=![]() x2��
x2��![]() x��n��n��������
x��n��n��������
��������y��������yn�Dz��ǡ�ͬ���������ߡ������ǣ���������ǵġ�ͬ���㡱����д������һ����ͬ��ͼ�����ʣ������ǣ���˵�����ɣ�
�ڵ�ֱ��y=![]() x+m��������y��yn���ཻ����4������ʱ����m��ȡֵ��Χ��
x+m��������y��yn���ཻ����4������ʱ����m��ȡֵ��Χ��
����ֱ��y=k��k<0����������y=��x2+2x+3��������yn =![]() x2��
x2��![]() x��n ��nΪ������������4�����㣬�����������α��Ϊ��A����B����C����D����AB=BC=CDʱ�����k��n֮��Ĺ�ϵʽ
x��n ��nΪ������������4�����㣬�����������α��Ϊ��A����B����C����D����AB=BC=CDʱ�����k��n֮��Ĺ�ϵʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ݰǼ�����ȫ����Զ�����⣬����Ϊ�����µ�һ������ij�ֵ��ݰǼ������Ϊÿǧ��40Ԫ����ÿǧ��60Ԫ���ۣ�ƽ��ÿ����۳�100ǧ�ˣ����������г����鷢�֣�����ÿ����2Ԫ����ƽ��ÿ���������������20ǧ�ˣ�����ר�����������ְǼ���Ҫƽ��ÿ�����2240Ԫ����ش�
��1��ÿǧ�����ְǼ�Ӧ���۶���Ԫ��
��2����ƽ��ÿ��������������£�Ϊ�����������ڹ˿ͣ��A���г����õ�Ӧ��ԭ�ۼ۵ļ��۳��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
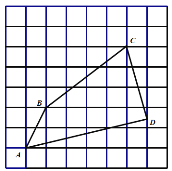
����Ŀ����ͼ����ÿ��С�����εı߳�Ϊ�������У���![]() ���ڸ���ϣ�
���ڸ���ϣ�![]() ΪС�����α��е㣮
ΪС�����α��е㣮
��1��![]() �ij����� ______��
�ij����� ______��
��2��������ͼ��ʾ�������У����̶ȵ�ֱ�ߣ�����һ����![]() ,ʹ������
,ʹ������![]() ˵����
˵����![]() ��λ��������ҵ���(��Ҫ��֤��)______��
��λ��������ҵ���(��Ҫ��֤��)______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������![]() �У�����P�ӵ�B������������B��C��D��B�˶������P������·��Ϊx��
�У�����P�ӵ�B������������B��C��D��B�˶������P������·��Ϊx��![]() �����Ϊy.��y����x�ĺ�����������ͼ����ͼ2��ʾ����ͼ2�е�a���ڣ� ��
�����Ϊy.��y����x�ĺ�����������ͼ����ͼ2��ʾ����ͼ2�е�a���ڣ� ��

A.25B.20C.12D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
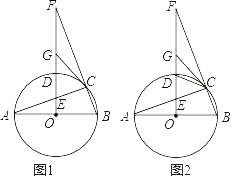
����Ŀ����ͼ1����֪AB����O��ֱ����AC����O���ң���O����OF��AB����O�ڵ�D����AC�ڵ�E����BC���ӳ����ڵ�F����G��EF���е㣬����CG
(1)�ж�CG����O��λ�ù�ϵ����˵�����ɣ�
(2)��֤��2OB2��BCBF��
(3)��ͼ2������DCE��2��F��CE��3��DG��2.5ʱ����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��վ���ͻ����ƽ��ʾ��ͼ��AD�����ļн�Ϊ60����Ϊ����ߴ����̵İ�ȫ�ԣ�����ʦ������С���ʹ������ļнǣ�ʹ����45�����37������˴��ʹ�����ص��ɵ�B����C��ǰ�ƶ���2��.

��1�����A�����ĸ߶ȣ�
��2�������Ҫ�ڻ����ŵص�C���������2�ף���ô���жϾ���D��14�Ļ���2�Ƿ���ҪŲ�ߣ���˵������.��sin37���0.6��cos37���0.8��tan37���0.75��![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com