
【题目】如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)判断CG与⊙O的位置关系,并说明理由;
(2)求证:2OB2=BCBF;
(3)如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.
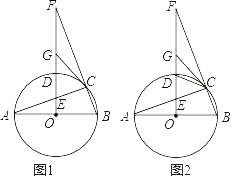
【答案】(1)CG与⊙O相切,理由见解析;(2)见解析;(3)DE=2
【解析】
(1)连接CE,由AB是直径知△ECF是直角三角形,结合G为EF中点知∠AEO=∠GEC=∠GCE,再由OA=OC知∠OCA=∠OAC,根据OF⊥AB可得∠OCA+∠GCE=90°,即OC⊥GC,据此即可得证;
(2)证△ABC∽△FBO得![]() ,结合AB=2BO即可得;
,结合AB=2BO即可得;
(3)证ECD∽△EGC得![]() ,根据CE=3,DG=2.5知
,根据CE=3,DG=2.5知![]() ,解之可得.
,解之可得.
解:(1)CG与⊙O相切,理由如下:
如图1,连接CE,
∵AB是⊙O的直径,
∴∠ACB=∠ACF=90°,
∵点G是EF的中点,
∴GF=GE=GC,
∴∠AEO=∠GEC=∠GCE,
∵OA=OC,
∴∠OCA=∠OAC,
∵OF⊥AB,
∴∠OAC+∠AEO=90°,
∴∠OCA+∠GCE=90°,即OC⊥GC,
∴CG与⊙O相切;
(2)∵∠AOE=∠FCE=90°,∠AEO=∠FEC,
∴∠OAE=∠F,
又∵∠B=∠B,
∴△ABC∽△FBO,
∴![]() ,即BOAB=BCBF,
,即BOAB=BCBF,
∵AB=2BO,
∴2OB2=BCBF;
(3)由(1)知GC=GE=GF,
∴∠F=∠GCF,
∴∠EGC=2∠F,
又∵∠DCE=2∠F,
∴∠EGC=∠DCE,
∵∠DEC=∠CEG,
∴△ECD∽△EGC,
∴![]() ,
,
∵CE=3,DG=2.5,
∴![]() ,
,
整理,得:DE2+2.5DE﹣9=0,
解得:DE=2或DE=﹣4.5(舍),
故DE=2.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:
①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.
其中正确的结论有
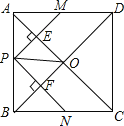
A.5个 B.4个 C.3个 D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A. 2B. 8C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
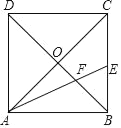
【题目】如图,正方形ABCD的边长为![]() +1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
(1)求证:△ABF∽△ACE;
(2)求tan∠BAE的值;
(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、C为半径是8的圆周上两动点,点B为![]() 的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为_____.
的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC、BC相切于点E、F,与AB分别相交于点G、H,且EH的延长线与CB的延长线交于点D,则CD的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD边长为4,M、N分别是BC、CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直,

(1)证明:Rt△ABM ∽Rt△MCN;
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式;当M点运动到什么位置时,四边形ABCN的面积最大,并求出最大面积;
(3)当M点运动到什么位置时Rt△ABM∽Rt△AMN,求此时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com