
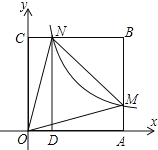
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴、y轴上,反比例函数![]() (k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,连接OM、ON、MN.若∠MON=45°,MN=2,则k的值为_______.
(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,连接OM、ON、MN.若∠MON=45°,MN=2,则k的值为_______.
【答案】![]()
【解析】
由反比例函数![]() (k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,易证得CN=AM,即可得△OAN≌△OAM,可得ON=OM,然后设作NE⊥OM于E点,易得△ONE为等腰直角三角形,设NE=x,则ON=
(k≠0,x>0)的图象与正方形的两边AB、BC分别交于点M、N,易证得CN=AM,即可得△OAN≌△OAM,可得ON=OM,然后设作NE⊥OM于E点,易得△ONE为等腰直角三角形,设NE=x,则ON=![]() x,由勾股定理可求得x的值,继而可设正方形ABCO的边长为a,则OC=a,CN=a-
x,由勾股定理可求得x的值,继而可设正方形ABCO的边长为a,则OC=a,CN=a-![]() ,则可得到点N的坐标,继而求得答案.
,则可得到点N的坐标,继而求得答案.
解:∵点M、N都在![]() 的图象上,
的图象上,
∴S△ONC=S△OAM=![]() k,即
k,即![]() OCNC=
OCNC=![]() OAAM,
OAAM,
∵四边形ABCO为正方形,
∴OC=OA,∠OCN=∠OAM=90°,
∴NC=AM,
在△OCN和△OAM中,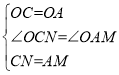 ,
,
∴△OCN≌△OAM(SAS);
∴ON=OM,
作NE⊥OM于E点,如图,
∵∠MON=45°,
∴△ONE为等腰直角三角形,
∴NE=OE,
设NE=x,则ON=![]() x,
x,
∴OM=![]() x,
x,
∴EM=![]() x-x=(
x-x=(![]() -1)x,
-1)x,
在Rt△NEM中,MN=2,
∵MN2=NE2+EM2,即22=x2+[(![]() -1)x]2,
-1)x]2,
∴x2=2+![]() ,
,
∴ON2=(![]() x)2=4+2
x)2=4+2![]() ,
,
∵CN=AM,CB=AB,
∴BN=BM,/span>
∴△BMN为等腰直角三角形,
∴BN=![]() MN=
MN=![]() ,
,
设正方形ABCO的边长为a,则OC=a,CN=a-![]() ,
,
∵在Rt△OCN中,OC2+CN2=ON2,
∴a2+(a-![]() )2=4+2
)2=4+2![]() ,
,
解得a1=![]() +1,a2=-1(舍去),
+1,a2=-1(舍去),
∴OC=![]() +1,
+1,
∴BC=OC=![]() +1,
+1,
∴CN=BC-BN=1,
∴N点坐标为(1,![]() +1),
+1),
将点N代入反比例函数![]() ,得:k=
,得:k=![]() +1.
+1.
故答案为![]() +1.
+1.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
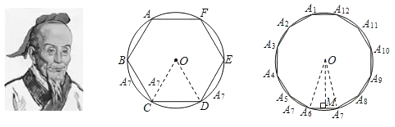
【题目】我国魏晋时期的数学家刘徽(263年左右)首创“割圆术”,所谓“割圆术”就是利用圆内接正多边形无限逼近圆来确定圆周率,刘徽计算出圆周率![]() .刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为
.刘微从正六边形开始分割圆,每次边数成倍增加,依次可得圆内接正十二边形,圆内接正二十四边形,…,割得越细,正多边形就越接近圆.设圆的半径为![]() ,圆内接正六边形的周长
,圆内接正六边形的周长![]() ,计算
,计算![]() ;圆内接正十二边形的周长
;圆内接正十二边形的周长![]() ,计算
,计算![]() ;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率
;那么分割到圆内接正二十四边形后,通过计算可以得到圆周率![]() __________.(参考数据:
__________.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
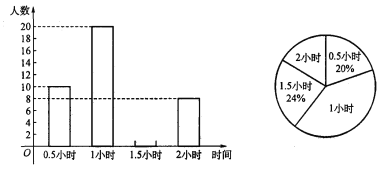
【题目】教育行政部门规定初中生每天户外活动的平均时间不少于1小时,为了解学生户外活动的情况,随机地对部分学生进行了抽样调查,并将调查结果绘制成如下两幅不完整的统计图.请根据图中提供的信息解答下列问题:
(1)在这次调查中共调查的学生人数为 ;活动时间为1小时所占的比例是 .
(2)补全条形统计图;
(3)若该市共有初中生约14000名,试估计该市符合教育行政部门规定的活动时间的学生数;
(4)如果从中任意抽取1名学生,活动时间为2小时的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019新型冠状病毒,因武汉病毒性肺炎病例而被发现,2020年1月12日被世界卫生组织命名“2019-nCoV”.冠状病毒是一个大型病毒家族,借助电子显微镜,我们可以看到这些病毒直径约为125纳米(1纳米=1 ![]() 10-9米),125纳米用科学记数法表示等于( )米
10-9米),125纳米用科学记数法表示等于( )米
A.1.25![]() 10-10B.1.25
10-10B.1.25![]() 10-11C.1.25
10-11C.1.25 ![]() 10-8D.1.25
10-8D.1.25![]() 10-7
10-7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班所有学生参加2010年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
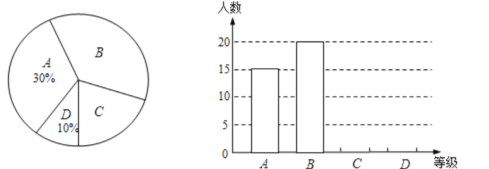
⑴ 九年级(1)班参加体育测试的学生有_________人;
⑵ 将条形统计图补充完整;
⑶ 在扇形统计图中,等级B部分所占的百分比是___,等级C对应的圆心角的度数为___°;
⑷ 若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有___人.
查看答案和解析>>
科目:初中数学 来源: 题型:
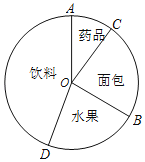
【题目】参加学校运动会,八年级1班第一天购买了水果,面包,饮料,药品等四种食品,四种食品购买金额的统计图表如图所示,若将水果、面包、药品三种食品统称为非饮料食品,并规定t=![]() .
.
(1)①求t的值;![]()
②求扇形统计图中钝角∠AOB的度数.
(2)根据实际需要,该班第二天购买这四种食品时,增加购买饮料金额,同时减少购买面包金额,假设增加购买饮料金额的25%等于减少购买面包的金额,且购买面包的金额不少于100元,求t的取值范围.
金额 食品 | 金额(单位:元) |
水果 | 100 |
面包 | 125 |
饮料 | 225 |
药品 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年,由于“疫情”的原因,学校未能准时开学,某中学为了了解学生在家“课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 6 |
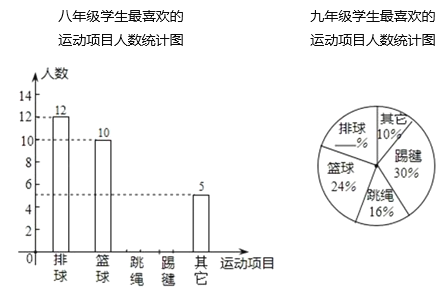
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取的人数为 人;
(2)请直接补全统计表和统计图;
(3)根据抽样调查的结果,请你估计该校1500名学生中有多少名学生最喜欢踢毽子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com