
【题目】定义:若两条抛物线在x轴上经过两个相同点,那么我们称这两条抛物线是“同交点抛物线”,在x轴上经过的两个相同点称为“同交点”,已知抛物线y=x2+bx+c经过(﹣2,0)、(﹣4,0),且一条与它是“同交点抛物线”的抛物线y=ax2+ex+f经过点(﹣3,3).
(1)求b、c及a的值;
(2)已知抛物线y=﹣x2+2x+3与抛物线yn=![]() x2﹣
x2﹣![]() x﹣n(n为正整数)
x﹣n(n为正整数)
①抛物线y和抛物线yn是不是“同交点抛物线”?若是,请求出它们的“同交点”,并写出它们一条相同的图像性质;若不是,请说明理由.
②当直线y=![]() x+m与抛物线y、yn,相交共有4个交点时,求m的取值范围.
x+m与抛物线y、yn,相交共有4个交点时,求m的取值范围.
③若直线y=k(k<0)与抛物线y=﹣x2+2x+3与抛物线yn =![]() x2﹣
x2﹣![]() x﹣n (n为正整数)共有4个交点,从左至右依次标记为点A、点B、点C、点D,当AB=BC=CD时,求出k、n之间的关系式
x﹣n (n为正整数)共有4个交点,从左至右依次标记为点A、点B、点C、点D,当AB=BC=CD时,求出k、n之间的关系式
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)①是“同交点抛物线”,“同交点”为:(–1,0)、(3,0),它们图形共同性质有:对称轴同为直线
;(2)①是“同交点抛物线”,“同交点”为:(–1,0)、(3,0),它们图形共同性质有:对称轴同为直线![]() ;②
;②![]() ,且
,且![]() ,
,![]() ;③
;③![]()
【解析】
(1)将(–2,0)、( –4,0)代入![]() ,即可求得b、c的值,设“同交点抛物线”的解析式为
,即可求得b、c的值,设“同交点抛物线”的解析式为![]() ,将(–3,3)代入即可求得
,将(–3,3)代入即可求得![]() 的值;
的值;
(2)①令![]() 和
和![]() ,分别求得与
,分别求得与![]() 轴的交点坐标,即可作出判断;
轴的交点坐标,即可作出判断;
②先求得直线![]() 与抛物线
与抛物线![]() 或抛物线
或抛物线![]() 只有一个交点时
只有一个交点时![]() 的值,除去直线
的值,除去直线![]() 经过“同交点”时的
经过“同交点”时的![]() 的值,即可求解;
的值,即可求解;
③由![]() 和
和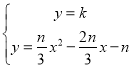 利用根与系数的关系求得
利用根与系数的关系求得![]() 和
和![]() 的值,再根据
的值,再根据![]() ,得到
,得到![]() 即可求得答案.
即可求得答案.
(1) ∵抛物线![]() 经过(–2,0)、( –4,0),则代入得:
经过(–2,0)、( –4,0),则代入得:![]() ,
,
解得:![]() ,
,![]() ,
,
设“同交点抛物线”的解析式为![]() ,
,
将(–3,3)代入得:![]() ,
,
解得:![]() ,
,
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)①令![]() ,则
,则![]() ,
,
解得:![]() ,
,
∴抛物线![]() 与
与![]() 轴的交点坐标为:(–1,0)、(3,0),
轴的交点坐标为:(–1,0)、(3,0),
令![]() ,则
,则![]()
![]()
![]()
![]() ,
,
解得:![]() ,
,
∴抛物线![]() 与
与![]() 轴的交点坐标为:(–1,0)、(3,0),
轴的交点坐标为:(–1,0)、(3,0),
∴抛物线![]() 和抛物线
和抛物线![]() 是“同交点抛物线”,
是“同交点抛物线”,
它们图形共同性质:对称轴同为直线![]() ;
;
②当直线![]() 与抛物线y相交只有1个交点时,
与抛物线y相交只有1个交点时,
由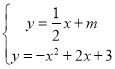 ,得:
,得:![]() ,
,
由![]() ,
,
解得:![]() ,
,
抛物线![]() 的顶点坐标为(1,
的顶点坐标为(1,![]() ),其中
),其中![]() 为正整数,
为正整数,
因为随着![]() 的增大,
的增大,![]() 的顶点纵坐标减小,所以当直线
的顶点纵坐标减小,所以当直线![]() 与抛物线
与抛物线![]() 中
中![]() 时的抛物线相交只有1个交点时,
时的抛物线相交只有1个交点时,
由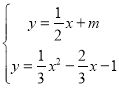 ,得:
,得:![]() ,
,
由![]() ,
,
解得:![]() ,
,
如图所示:
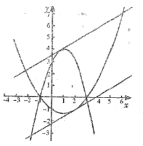
当直线![]() 经过“同交点”时与两抛物线只有三个交点,
经过“同交点”时与两抛物线只有三个交点,
把“同交点”(–1,0)代入![]() 得:
得:![]() ,
,
把“同交点” (3,0)代入![]() 得:
得:![]() ,
,
∴当直线![]() 与抛物线
与抛物线![]() 、
、![]() 有4个交点时,m的取值范围为:
有4个交点时,m的取值范围为:
![]() ,且
,且![]() ,
,![]() ;
;
③设直线![]() 分别与抛物线
分别与抛物线![]() 和抛物线
和抛物线![]() 相交于A、D、B、C,如图:
相交于A、D、B、C,如图:
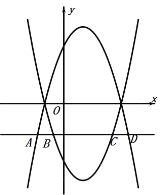
由![]() ,得:
,得:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
由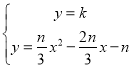 ,得:
,得:![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3![]() ,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_____.
,BC=12,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A'处,若AO=OB=2,则图中阴影部分面积为_____.
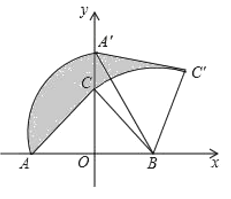
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数ymxn与反比例函数y![]() 同时经过点P(x,y)则称二次函数ymx2nxk为一次函数与反比例函数的“共享函数”,称点P为共享点.
同时经过点P(x,y)则称二次函数ymx2nxk为一次函数与反比例函数的“共享函数”,称点P为共享点.
(1)判断y2x1与y![]() 是否存在“共享函数”,如果存在,请求出“共享点”.如果不存在,请说明理由;
是否存在“共享函数”,如果存在,请求出“共享点”.如果不存在,请说明理由;
(2)已知:整数m,n,t满足条件t<n<8m,并且一次函数y=(1+n)x+2m+2与反比例函数y![]() 存在“共享函数”y=(m+t)x2+(10mt)x2020,求m的值.
存在“共享函数”y=(m+t)x2+(10mt)x2020,求m的值.
(3)若一次函数yxm和反比例函数y![]() 在自变量x的值满足mxm6的情况下,其“共享函数”的最小值为3,求其“共享函数”的解析式.
在自变量x的值满足mxm6的情况下,其“共享函数”的最小值为3,求其“共享函数”的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,随着电子产品的广泛应用,学生的近视发生率出现低龄化趋势,引起了相关部门的重视.某区为了了解在校学生的近视低龄化情况,对本区7-18岁在校近视学生进行了简单的随机抽样调查,并绘制了以下两幅不完整的统计图.

请根据图中信息,回答下列问题:
(1)这次抽样调查中共调查了近视学生 人;
(2)请补全条形统计图;
(3)扇形统计图中10-12岁部分的圆心角的度数是 ;
(4)据统计,该区7-18岁在校学生近视人数约为10万,请估计其中7-12岁的近视学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,BG与⊙O相切于点B,交AC的延长线于点D(点D在线段BG上),AC = 8,tan∠BDC =![]()
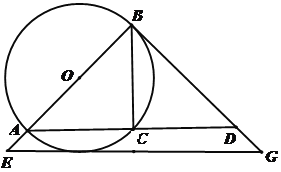
(1)求⊙O的直径;
(2)当DG=![]() 时,过G作
时,过G作![]() ,交BA的延长线于点E,说明EG与⊙O相切.
,交BA的延长线于点E,说明EG与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
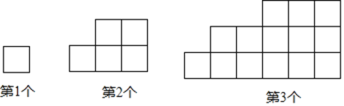
【题目】下列图形都是由大小相同的小正方形按一定规律组成的,其中第1个图形的周长为4,第2个图形的周长为10,第3个图形的周长为18,…,按此规律排列,回答下列问题:
(1)第5个图形的周长为 ;
(2)第![]() 个图形的周长为 ;
个图形的周长为 ;
(3)若第![]() 个图形的周长为180,则
个图形的周长为180,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
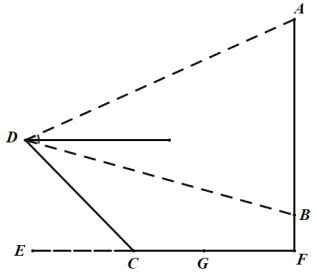
【题目】如图,为测量瀑布![]() 的高度,测量人员在瀑布对面山上的
的高度,测量人员在瀑布对面山上的![]() 点处测得瀑布顶端
点处测得瀑布顶端![]() 点的仰角是
点的仰角是![]() ,测得瀑布底端
,测得瀑布底端![]() 点的俯角是
点的俯角是![]() ,
,![]() 与水平面垂直.又在瀑布下的水平面测得
与水平面垂直.又在瀑布下的水平面测得![]() ,
,![]() (注:
(注:![]() 、
、![]() 、
、![]() 三点在同一直线上,
三点在同一直线上,![]() 于点
于点![]() ),斜坡
),斜坡![]() ,坡角
,坡角![]() ,那么瀑布
,那么瀑布![]() 的高度约为( ).(精确到
的高度约为( ).(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
A.![]()
![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com