
【题目】如图,AD为△ABC的中线,BE为△ABD的中线,
(1)若∠ABE=25°,∠BAD=50°,则∠BED的度数是 度.
(2)在△ADC中过点C作AD边上的高CH.
(3)若△ABC的面积为60,BD=5,求点E到BC边的距离.
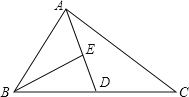
【答案】(1)75;(2)作图见解析;(3)点E到BC边的距离为6.
【解析】
(1)根据三角形的一个外角等于与它不相邻的两个内角和,∠BED=∠ABE+∠BAE=75°;
(2)三角形高的基本作法:用圆规以一边两端点为圆心,任意长为半径作两段弧,交于角的两边,再以交点为圆心,用交轨法作两段弧,找到两段弧的交点,连接两个交点,并过另一端点作所成直线的平行线,叫该边所在直线一点,连接该点和另一端点,则为高线;
(3)我们通过证明不难得出三角形中线将三角形分成面积相等的两个三角形,那么可依据D是BC中点,E是AD中点,求出三角形BED的面积.三角形BDE中,E到BD的距离就是BD边上的高,有了三角形BDE的面积,BD的长也容易求得.那么高就求出来了.
(1)∠BED=∠ABE+∠BAE=75°;
(2)
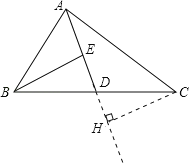
CH为所求的高.
(3)如图,过点E作EF⊥BD于点F,
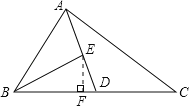
∵AD是BC的中线
∴BD=CD
∴![]()
同理![]()
又∵![]()
∴EF=6
即点E到BC边的距离为6.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
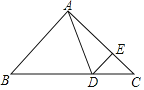
【题目】如图,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连结DE.
(1)当∠BAD=60°,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试写出∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
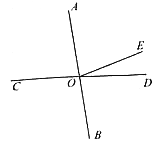
【题目】如图,AB、CD交于点O,∠AOE=4∠DOE,∠AOE的余角比∠DOE小10°(题中所说的角均是小于平角的角).
(1)求∠AOE的度数;
(2)请写出∠AOC在图中的所有补角;
(3)从点O向直线AB的右侧引出一条射线OP,当∠COP=∠AOE+∠DOP时,求∠BOP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
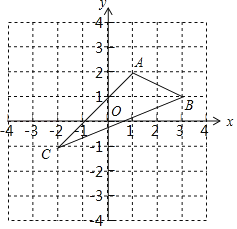
【题目】如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)直接写出点A1,B1,C1的坐标.
A1 , B1 , C1 ;
(3)请你求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7) 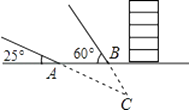
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( ) 
A.当行驶速度为40km/h时,每消耗1升汽油,甲车能行驶20km
B.消耗1升汽油,丙车最多可行驶5km
C.当行驶速度为80km/h时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同
D.当行驶速度为60km/h时,若行驶相同的路程,丙车消耗的汽油最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
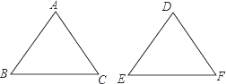
A. ∠B=∠E,BC=EF B. ∠A=∠D,BC=EF
C. ∠A=∠D,∠B=∠E D. BC=EF,AC=DF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com