
【题目】如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
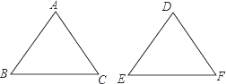
A. ∠B=∠E,BC=EF B. ∠A=∠D,BC=EF
C. ∠A=∠D,∠B=∠E D. BC=EF,AC=DF
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
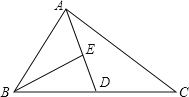
【题目】如图,AD为△ABC的中线,BE为△ABD的中线,
(1)若∠ABE=25°,∠BAD=50°,则∠BED的度数是 度.
(2)在△ADC中过点C作AD边上的高CH.
(3)若△ABC的面积为60,BD=5,求点E到BC边的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把直角三角形纸片沿过顶点B的直线(BE交CA于E)折叠,直角顶点C落在斜边AB上,如果折叠后得等腰△EBA,那么结论中:①∠A=30°;②点C与AB的中点重合;③点E到AB的距离等于CE的长,正确的个数是( )
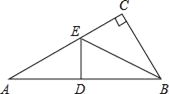
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+4a﹣3(a≠0)的顶点为A. 
(1)求顶点A的坐标;
(2)过点(0,5)且平行于x轴的直线l,与抛物线y=ax2﹣4ax+4a﹣3(a≠0)交于B,C两点. ①当a=2时,求线段BC的长;
②当线段BC的长不小于6时,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )
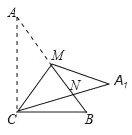
A. 30° B. 36° C. 50° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
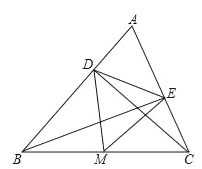
【题目】已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.
(1) 若DE=3,BC=8,求△DME的周长;
(2) 若∠A=60°,求证:∠DME=60°;
(3) 若BC2=2DE2,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如下图所示),并用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题.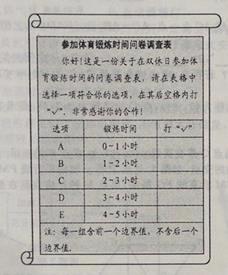
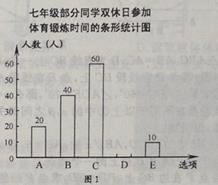
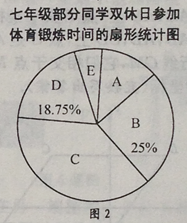
(1)本次接受问卷调查的同学有多少人?补全条形统计图.
(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
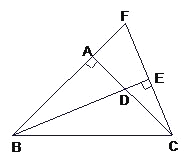
【题目】如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com