
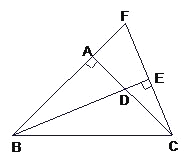
【题目】如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.
【答案】见解析。
【解析】
求出∠FBE=∠CBE,∠BEF=∠BEC=90°,根据ASA可证明Rt△BEF≌Rt△BEC,即可得CF=2CE,由等腰直角三角形的性质可得∠ABC=∠ACB=45°,根据BD是∠ABC的平分线可得∠F=∠ADB=67.5°,通过AAS可证明△ABD≌△ACF,根据全等三角形性质可得BD=CF,即可证明BD=2CE.
∵BD是∠ABC的平分线,
∴∠FBE=∠CBE,
∵BE⊥CF,
∴∠BEF=∠BEC=90°,
在Rt△BEF和Rt△BEC中,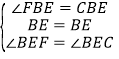 ,
,
∴Rt△BEF≌Rt△BEC(ASA).
∴CE=EF,
∴CF=2CE,
∵∠BAC=90°,且AB=AC,
∴∠FAC=∠BAC=90°,∠ABC=∠ACB=45°,
∵BD是∠ABC的平分线,
∴∠FBE=∠CBE=22.5°,
∴∠F=90°-22.5°=67.5°,∠ADB=90°-22.5°=67.5°,
∴∠F=∠ADB,
在△ABD和△ACF中,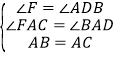 ,
,
∴△ABD≌△ACF(AAS),
∴BD=CF,
∵CF=2CE,
∴BD=2CE.


科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( ) 
A.当行驶速度为40km/h时,每消耗1升汽油,甲车能行驶20km
B.消耗1升汽油,丙车最多可行驶5km
C.当行驶速度为80km/h时,每消耗1升汽油,乙车和丙车行驶的最大公里数相同
D.当行驶速度为60km/h时,若行驶相同的路程,丙车消耗的汽油最少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
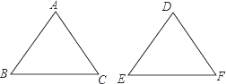
A. ∠B=∠E,BC=EF B. ∠A=∠D,BC=EF
C. ∠A=∠D,∠B=∠E D. BC=EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的角平分线上一点,过P作PC//OA交OB于点C.若∠AOB=30°,OC=4cm,则点P到OA的距离PD等于___________cm.
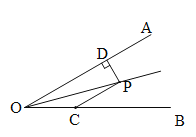
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°.②求α,β之间的关系式.
(2)是否存在不同于以上②中的α,β之间的关系式?若存在,请求出这个关系式(求出一个即可);若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )
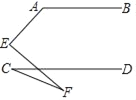
A. ∠A=∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F=180°
C. ∠A﹣∠E+∠C+∠F=90° D. ∠A+∠E+∠C+∠F=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学团委会开展书法、诵读、演讲、征文四个项目(每人只参加一个项目)的比赛,初三(1)班全体同学都参加了比赛,为了解比赛的具体情况,小明收集整理数据后,绘制了以下不完整的折线统计图和扇形统计图,根据图表中的信息解答下列各题: 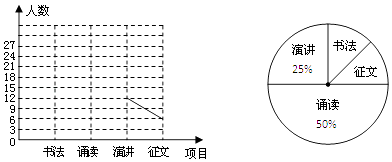
(1)初三(1)班的总人数为 , 扇形统计图中“征文”部分的圆心角度数为度;
(2)请把折线统计图补充完整;
(3)平平和安安两个同学参加了比赛,请用“列表法”或“画树状图法”,求出他们参加的比赛项目相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,各自到达终点后停止行驶。设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,则两车相遇之后又经过___________小时,两车相距720km.
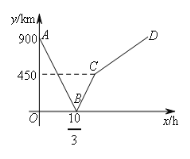
查看答案和解析>>
科目:初中数学 来源: 题型:
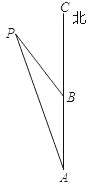
【题目】如图,一艘轮船从点 A 向正北方向航行,每小时航行 15 海里,小岛P 在轮船的北偏西 15°,3 小时后轮船航行到点 B,小岛 P 此时在轮船的北偏西 30°方向,在小岛 P 的周围 20 海里范围内有暗礁,如果轮船不改变方向继续向前航行,是否会有触礁危险?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com