
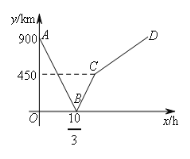
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,各自到达终点后停止行驶。设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,则两车相遇之后又经过___________小时,两车相距720km.
【答案】![]()
【解析】
先求出快车和慢车的车速,根据图形信息确定![]() h两车相遇,第5小时,快车到达终点停止运动,此时两车相距450km,因此只要慢车再走270km辆车就会相距720km.求出慢车所用的总时间与相遇时的时间相减即可.
h两车相遇,第5小时,快车到达终点停止运动,此时两车相距450km,因此只要慢车再走270km辆车就会相距720km.求出慢车所用的总时间与相遇时的时间相减即可.
解:由图可知A(0,900),B(![]() ,0)
,0)
∴直线AB解析式为:y=-270x+900,
由题可知AB与BC的速度不变,
∴设BC段的函数解析式为y=270x+b,
代入B(![]() ,0),得b=-900,
,0),得b=-900,
∴直线BC解析式为:y=270x-900,
∴C(5,450)
∴慢车的速度 450![]() 5=90km/h,
5=90km/h,
快车的速度![]() 90
90![]() (5-
(5-![]() )=180km/h,
)=180km/h,
∴第5小时,快车到达终点停止运动,此时两车相距450km,
∴720![]() 90=8,即第8小时两车相距720km,
90=8,即第8小时两车相距720km,
∴8-![]() ,
,
故答案是![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+4a﹣3(a≠0)的顶点为A. 
(1)求顶点A的坐标;
(2)过点(0,5)且平行于x轴的直线l,与抛物线y=ax2﹣4ax+4a﹣3(a≠0)交于B,C两点. ①当a=2时,求线段BC的长;
②当线段BC的长不小于6时,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
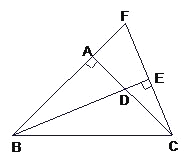
【题目】如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
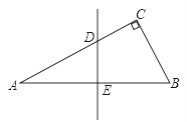
【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是________
查看答案和解析>>
科目:初中数学 来源: 题型:
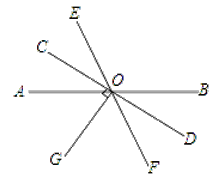
【题目】如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=36°.
(1)求∠AOG的度数;
(2)若OG是∠AOF的平分线,那么OC是∠AOE的平分线吗?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
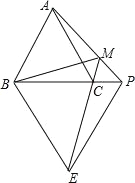
【题目】如图,已知等边△ABC 和等边△BPE,点 P 在 BC 的延长线上,EC 的延长线交 AP 于点 M,连接 BM;下列结论:①AP=CE;②∠PME=60°;③BM 平分∠AME;④AM+MC=BM,其中正确的有____________________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com