
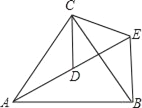
【题目】如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.
(1)求证:AD=BE;
(2)求∠AEB的度数.
【答案】(1)证明见解析;(2)∠AEB=60°.
【解析】(1)根据等边三角形的性质得出AC=BC,CD=CE,∠ACB=∠DCE=60°,求出∠ACD=∠BCE,然后根据SAS证明△ACD≌△BCE,即可得出AD=BE;
(2)由△ECD是等边三角形可得∠CDE=∠CED=60°,根据补角的性质可求∠ADC=120°,根据全等三角形的性质可得∠BEC=∠ADC=120°,进而根据∠AEB=∠BEC﹣∠CED可得出答案.
证明:(1)∵△ACB和△ECD都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
又∵∠ACD=∠ACB﹣∠DCB,∠BCE=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
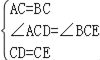
∴△ACD≌△BCE(SAS).
∴AD=BE;
(2)在等边△ECD中,
∠CDE=∠CED=60°,
∴∠ADC=120°,
∵△ACD≌△BCE,
∴∠BEC=∠ADC=120°,
∴∠AEB=∠BEC﹣∠CED=120°﹣60°=60°.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上. 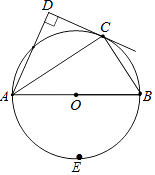
(1)求证:CD是⊙O的切线;
(2)点E是⊙O上一点,连接BE,CE.若∠BCE=42°,cos∠DAC= ![]() ,AC=m,写出求线段CE长的思路.
,AC=m,写出求线段CE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
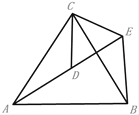
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°.②求α,β之间的关系式.
(2)是否存在不同于以上②中的α,β之间的关系式?若存在,请求出这个关系式(求出一个即可);若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学团委会开展书法、诵读、演讲、征文四个项目(每人只参加一个项目)的比赛,初三(1)班全体同学都参加了比赛,为了解比赛的具体情况,小明收集整理数据后,绘制了以下不完整的折线统计图和扇形统计图,根据图表中的信息解答下列各题: 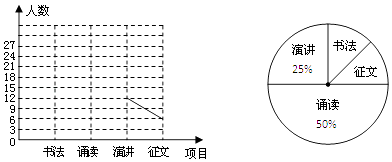
(1)初三(1)班的总人数为 , 扇形统计图中“征文”部分的圆心角度数为度;
(2)请把折线统计图补充完整;
(3)平平和安安两个同学参加了比赛,请用“列表法”或“画树状图法”,求出他们参加的比赛项目相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,各自到达终点后停止行驶。设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,则两车相遇之后又经过___________小时,两车相距720km.
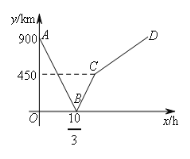
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线l和直线l外一点P.
求作:直线l的平行直线,使它经过点P.
作法:如图2.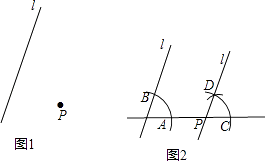
(i)过点P作直线m与直线l交于点O;
(ii)在直线m上取一点A(OA<OP),以点O为圆心,OA长为半径画弧,与直线l交于点B;
(iii)以点P为圆心,OA长为半径画弧,交直线m于点C,以点C为圆心,AB长为半径画弧,两弧交于点D;
(iv)作直线PD.
所以直线PD就是所求作的平行线.
请回答:该作图的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
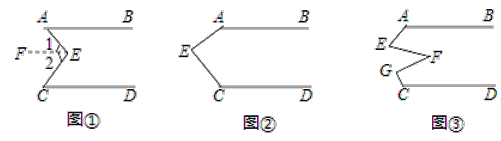
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BEE+∠DCE=∠AEC.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式):
解:如图①,过点E作EF∥AB
∴∠BAE=∠1( )
∵AB∥CD( )
∴CD∥EF( )
∴∠2=∠DCE
∴∠BAE+∠DCE=∠1+∠2( )
∴∠BAE+∠DCE=∠AEC
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠FGC+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③.若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象经过点(-3,-2).
的图象经过点(-3,-2).
(1)求这个函数表达式;
(2)判断(-5,3)是否在这个函数的图象上.
(3)点M在直线y=kx+4上且到y轴的距离是3,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com