
����Ŀ����һ�����ǰ��е�����ֱ�����ǰ��ֱ�Ƕ���C����ͼ��ʽ������һ��������ʾ����A��60�㣬��D��30�㣬��E����B��45�㣮
(1)������DCB��45�㣬���ACB�Ķ���Ϊ�� ����
������ACB��140�㣬���DCE�Ķ���Ϊ�� ����
(2)��(1)�����ACB���DCE��������ϵ����˵�����ɣ�
(3)����ACE��90���ҵ�E��ֱ��AC���Ϸ�ʱ�������������dz���һ�����ƽ��ʱ����ֱ��д����ACE�Ƕ����п��ܵ�ֵ(����˵������)��

���𰸡�(1)��135�㣻��40�㣻(2)��ACB+��DCE��180�㣬���ɼ�������(3)30�㡢45�㣮
��������
(1)�ٸ���ֱ�����ǰ�����ʽ����DCB��45�����ɵó���ACB�Ķ�����
���ɡ�ACB=140�㣬��ECB=90�㣬�ɵó���ACE�Ķ����������ó���DCE�Ķ�����
(2)���ݢ��еĽ��ۿ�������룬���ɡ�ACB=��ACD+��DCB����ACB+��DCE=90��+��DCB+��DCE�ɵó����ۣ�
(3)��CB��AD��EB��AC��������������ۼ���.
(1)�١ߡ�DCB��45������ACD��90����
���ACB����DCB+��ACD��45��+90����135����
�ʴ�Ϊ��135����
�ڡߡ�ACB��140������ECB��90����
���ACE��140����90����50����
���DCE��90������ACE��90����50����40����
�ʴ�Ϊ��40����
(2)���룺��ACB+��DCE��180����
�������£��ߡ�ACE��90������DCE��
���ߡ�ACB����ACE+90����
���ACB��90������DCE+90����180������DCE��
����ACB+��DCE��180����
(3)30����45����
���ɣ���CB��ADʱ����ͼ1����
����AFC=��FCB=90����
����A=60����
����ACE��90��-��A=30����
��EB��ACʱ����ͼ2����
���ACE����E=45����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1=��2��AC=AD��������һ��������ʹ��ABC�ա�AED�������ӵ�������______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У������²�����ͼ���ٷֱ���A��BΪԲ�ģ����� ![]() AB�ij�Ϊ�뾶�����������ཻ�ڵ�M��N������ֱ��MN��AC�ڵ�D������BD����CD=CB����A=35�㣬���C���ڣ� ��
AB�ij�Ϊ�뾶�����������ཻ�ڵ�M��N������ֱ��MN��AC�ڵ�D������BD����CD=CB����A=35�㣬���C���ڣ� �� 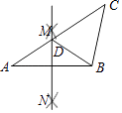
A.40��
B.50��
C.60��
D.70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ1��ֱ��MN��ֱ��AB��CD�ֱ��ڵ�E��F����1���2������
(1)���ж�ֱ��AB��CD��λ�ù�ϵ����˵�����ɣ�
(2)��ͼ2����BEF���EFD�Ľ�ƽ���߽��ڵ�P��EP��CD���ڵ�G����H��MN�ϵ�һ����GH��EG����֤��PF��GH��
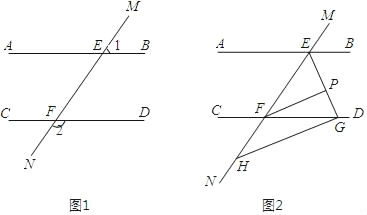
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACB����ECD���ǵȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��1����֤��AD=BE��
��2�����AEB�Ķ�����
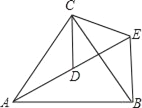
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������AM��BN���߶�CD�������˵�C��D�ֱ�������BN��AM�ϣ��ҡ�A����BCD��108�㣮E���߶�AD��һ�㣨�����A��D�غϣ�����BDƽ�֡�EBC��
��1�����ABC�Ķ�����
��2������ͼ���ҳ����ABC��ȵĽǣ���˵�����ɣ�
��3����ƽ���ƶ�CD����AD��CD�����ADB���AEB�Ķ���֮���Ƿ�����CDλ�õı仯�������仯�����仯���ҳ��仯���ɣ������䣬��������ֵ��
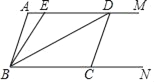
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ס����������90km��A��B������ͬһ��·�Ӽس������ҵأ�A��Ħ�г���B��綯����ͼ��DE��OC�ֱ��ʾA��B�뿪�ص�·��s��km����ʱ��t��h���ĺ�����ϵ��ͼ����ͼ�����������⣮
��1��A��B���������Сʱ��B���ٶ��Ƕ��٣�
��2����B������Сʱ������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E��F��ֱ��AB�ϣ���G���߶�CD�ϣ�ED��FG���ڵ�H����C����EFG����CED����GHD��
��1����֤��CE��GF��
��2�����жϡ�AED���D֮���������ϵ����˵�����ɣ�
��3������EHF��80������D��30�������AEM�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com