
【题目】如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上. 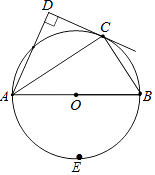
(1)求证:CD是⊙O的切线;
(2)点E是⊙O上一点,连接BE,CE.若∠BCE=42°,cos∠DAC= ![]() ,AC=m,写出求线段CE长的思路.
,AC=m,写出求线段CE长的思路.
【答案】
(1)解:证明:连接OC,如图1中.
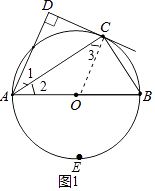
∵AC平分∠DAB,
∴∠1=∠2,
∵OA=OC,
∴∠3=∠2,
∴∠3=∠1,
∴AD∥OC,
∴∠OCD=∠D=90°,
又∵OC是⊙O的半径,
∴CD是⊙O的切线.
(2)解:求解思路如下:
过点B作BF⊥CE于F,如图.
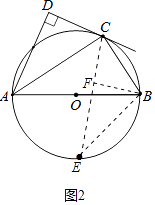
①在Rt△ACB中,根据BC=ACtan∠CAB,求出BC.
②在Rt△CFB中,由∠BCF=42°及BC的长,可求CF,BF的长;
③在Rt△EFB中,由∠E的三角函数值及BF的长,可EF的长;
④由CE=CF+EF,可求CE的长
【解析】(1)连接OC,如图1中.只要证明OC∥AD,由AD⊥CD,即可证明OC⊥CD解决问题.(2)过点B作BF⊥CE于F,如图2中.①在Rt△ACB中,根据BC=ACtan∠CAB,求出BC.②在Rt△CFB中,由∠BCF=42°及BC的长,可求CF,BF的长;③在Rt△EFB中,由∠E的三角函数值及BF的长,可EF的长;④由CE=CF+EF,可求CE的长.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与反比例函数y= ![]() (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=
(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα= ![]() .
. 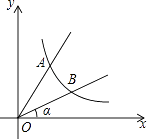
(1)求k的值.
(2)求点B的坐标.
(3)设点P(m,0),使△PAB的面积为2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( ) 
A.30千米/小时
B.18千米/小时
C.15千米/小时
D.9千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把直角三角形纸片沿过顶点B的直线(BE交CA于E)折叠,直角顶点C落在斜边AB上,如果折叠后得等腰△EBA,那么结论中:①∠A=30°;②点C与AB的中点重合;③点E到AB的距离等于CE的长,正确的个数是( )
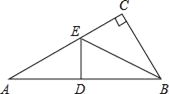
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+4a﹣3(a≠0)的顶点为A. 
(1)求顶点A的坐标;
(2)过点(0,5)且平行于x轴的直线l,与抛物线y=ax2﹣4ax+4a﹣3(a≠0)交于B,C两点. ①当a=2时,求线段BC的长;
②当线段BC的长不小于6时,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A的度数是( )
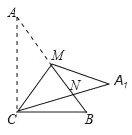
A. 30° B. 36° C. 50° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如下图所示),并用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题.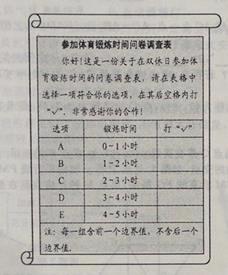
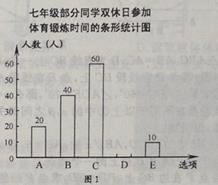
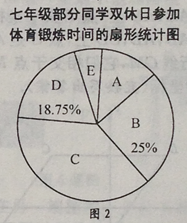
(1)本次接受问卷调查的同学有多少人?补全条形统计图.
(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com