
【题目】如图,直线y=2x与反比例函数y= ![]() (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=
(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα= ![]() .
. 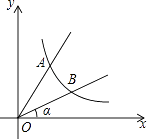
(1)求k的值.
(2)求点B的坐标.
(3)设点P(m,0),使△PAB的面积为2,求m的值.
【答案】
(1)解:把点A(1,a)代入y=2x,
得a=2,
则A(1,2).
把A(1,2)代入y= ![]() ,得k=1×2=2;
,得k=1×2=2;
(2)解:过B作BC⊥x轴于点C.
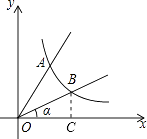
∵在Rt△BOC中,tanα= ![]() ,
,
∴可设B(2h,h).
∵B(2h,h)在反比例函数y= ![]() 的图象上,
的图象上,
∴2h2=2,解得h=±1,
∵h>0,∴h=1,
∴B(2,1);
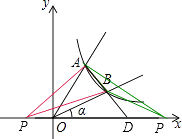
(3)解:∵A(1,2),B(2,1),
∴直线AB的解析式为y=﹣x+3,
设直线AB与x轴交于点D,则D(3,0).
∵S△PAB=S△PAD﹣S△PBD=2,点P(m,0),
∴ ![]() |3﹣m|×(2﹣1)=2,
|3﹣m|×(2﹣1)=2,
解得m1=﹣1,m2=7.
【解析】(1)把点A(1,a)代入y=2x,求出a=2,再把A(1,2)代入y= ![]() ,即可求出k的值;(2)过B作BC⊥x轴于点C.在Rt△BOC中,由tanα=
,即可求出k的值;(2)过B作BC⊥x轴于点C.在Rt△BOC中,由tanα= ![]() ,可设B(2h,h).将B(2h,h)代入y=
,可设B(2h,h).将B(2h,h)代入y= ![]() ,求出h的值,即可得到点B的坐标;(3)由A(1,2),B(2,1),利用待定系数法求出直线AB的解析式为y=﹣x+3,那么直线AB与x轴交点D的坐标为(3,0).根据△PAB的面积为2列出方程
,求出h的值,即可得到点B的坐标;(3)由A(1,2),B(2,1),利用待定系数法求出直线AB的解析式为y=﹣x+3,那么直线AB与x轴交点D的坐标为(3,0).根据△PAB的面积为2列出方程 ![]() |3﹣m|×(2﹣1)=2,解方程即可求出m的值.
|3﹣m|×(2﹣1)=2,解方程即可求出m的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
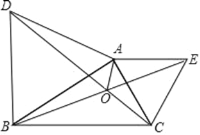
【题目】如图,分别以△ABC 的边 AB,AC 向外作等边三角形 ABD 和等边三角形 ACE,线段 BE 与 CD 相交于点 O,连接 OA.
(1)求证:BE=DC;
(2)求∠BOD 的度数;
(3)求证:OA 平分∠DOE.
(4)猜想线段 OA、OB、OD 的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒,已知购买一个台灯比购买一个手电筒多用20元,若用400元购买台灯和用160元购买手电筒,则购买台灯的个数是购买手电筒个数的一半.
(1)求购买该品牌一个台灯、一个手电筒各需要多少元?
(2)经商谈,商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠,如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个,且该公司购买台灯和手电筒的总费用不超过670元,那么荣庆公司最多可购买多少个该品牌台灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级![]() 班数学课外兴趣小组在探究:“
班数学课外兴趣小组在探究:“![]() 边形共有多少条对角线”这一问题时,设计了如下表格:
边形共有多少条对角线”这一问题时,设计了如下表格:
多边形的边数 |
|
|
|
|
| … |
从多边形一个顶点出发可引起的对角线条数 | … | |||||
多边形对角线的总条数 | … |
![]() 探究:假若你是该小组的成员,请把你研究的结果填入上表;
探究:假若你是该小组的成员,请把你研究的结果填入上表;
![]() 猜想:随着边数的增加,多边形对角线的条数会越来越多,从
猜想:随着边数的增加,多边形对角线的条数会越来越多,从![]() 边形的一个顶点出发可引的对角线条数为多少,
边形的一个顶点出发可引的对角线条数为多少,![]() 边形对角线的总条数为多少.
边形对角线的总条数为多少.
![]() 应用:
应用:![]() 个人聚会,每不相邻的人都握一次手,共握多少次手?
个人聚会,每不相邻的人都握一次手,共握多少次手?
查看答案和解析>>
科目:初中数学 来源: 题型:
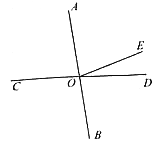
【题目】如图,AB、CD交于点O,∠AOE=4∠DOE,∠AOE的余角比∠DOE小10°(题中所说的角均是小于平角的角).
(1)求∠AOE的度数;
(2)请写出∠AOC在图中的所有补角;
(3)从点O向直线AB的右侧引出一条射线OP,当∠COP=∠AOE+∠DOP时,求∠BOP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
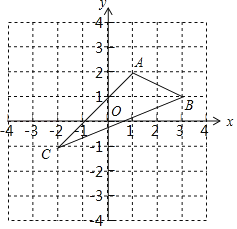
【题目】如图,在平面直角坐标系中,已知A(1,2),B(3,1),C(﹣2,﹣1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1.
(2)直接写出点A1,B1,C1的坐标.
A1 , B1 , C1 ;
(3)请你求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某探测队在地面A、B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5, ![]() ≈1.7)
≈1.7) 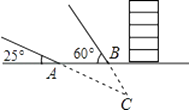
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠D=90°,AC平分∠DAB,且点C在以AB为直径的⊙O上. 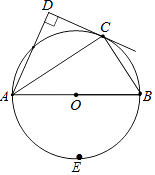
(1)求证:CD是⊙O的切线;
(2)点E是⊙O上一点,连接BE,CE.若∠BCE=42°,cos∠DAC= ![]() ,AC=m,写出求线段CE长的思路.
,AC=m,写出求线段CE长的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com