
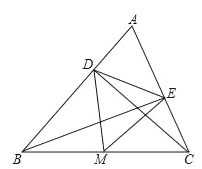
【题目】已知锐角△ABC中,CD,BE分别是AB,AC边上的高,M是线段BC的中点,连接DM,EM.
(1) 若DE=3,BC=8,求△DME的周长;
(2) 若∠A=60°,求证:∠DME=60°;
(3) 若BC2=2DE2,求∠A的度数.
【答案】(1)11;(2)见解析(3)∠A=45°
【解析】
试题(1)由三角形的高可以得到∠CDB=∠BEC=90°,再由直角三角形的斜边上的中点得出DM和EM的长,从而得结果.
(2)由直角三角形的斜边上的中点得出DM和EM的长,从而得DM=BM,EM=CM,进而得到∠DME=60°,
(3)由DM=EM=![]() BC,
BC,![]() 得
得![]() ,得到△DEM,从而求出结果.
,得到△DEM,从而求出结果.
试题解析:(1)∵∠CDB=∠BEC=90°,点M为BC的中点,
∴DM=EM=![]() BC=4,
BC=4,
又∵DE=3,
∴△DME的周长=DM+EM+DE=11;
(2)∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵DM=EM=![]() BC,
BC,
∴DM=BM,EM=CM,
∴∠DMB=180°-2∠ABC,∠EMC=180°-2∠ACB,
∴∠DME=180°-∠DMB-∠EMC=2(∠ABC+∠ACB)-180°,
∴∠DME=60°;
(3)∵DM=EM=![]() BC,BC2=2DE2,
BC,BC2=2DE2,
∴DM2=EM2=![]() DE2,
DE2,
∴![]() ,
,
∴∠DME=90°,
∴∠DMB+∠EMC=90°,
∵∠DMB=180°-2∠ABC,∠EMC=180°-2∠ACB,
∴∠ABC+∠ACB=135°,
∴∠A=45°


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 若|a|=﹣a,则 a 一 定是负数
B. 单项式 x3y2z 的系数为 1,次数是 6
C. 若 AP=BP,则点 P 是线段 AB 的中点
D. 若∠AOC=![]() ∠AOB,则射线 OC 是∠AOB 的平分线
∠AOB,则射线 OC 是∠AOB 的平分线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点![]() 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )
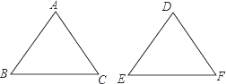
A. ∠B=∠E,BC=EF B. ∠A=∠D,BC=EF
C. ∠A=∠D,∠B=∠E D. BC=EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.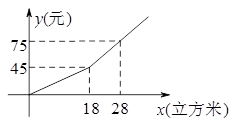
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式.若小敏家某月交水费81元,则这个月用水量为多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
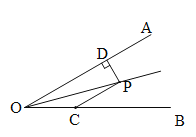
【题目】如图,点P是∠AOB的角平分线上一点,过P作PC//OA交OB于点C.若∠AOB=30°,OC=4cm,则点P到OA的距离PD等于___________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,则∠A、∠C、∠E、∠F满足的数量关系是( )
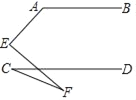
A. ∠A=∠C+∠E+∠F B. ∠A+∠E﹣∠C﹣∠F=180°
C. ∠A﹣∠E+∠C+∠F=90° D. ∠A+∠E+∠C+∠F=360°
查看答案和解析>>
科目:初中数学 来源: 题型:
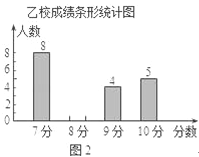
【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
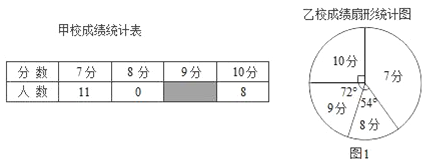
(1)在图1中,“7分”所在扇形的圆心角等于 °.
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com