
 如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE,联结BG并延长与AC交于点F,如果AD=9,CE=12,那么下列结论不正确的是( )
如图,△ABC的两条中线AD、CE交于点G,且AD⊥CE,联结BG并延长与AC交于点F,如果AD=9,CE=12,那么下列结论不正确的是( )| A. | AC=10 | B. | AB=15 | C. | BG=10 | D. | BF=15 |
分析 根据题意得到点G是△ABC的重心,根据重心的性质得到AG=$\frac{2}{3}$AD=6,CG=$\frac{2}{3}$CE=8,EG=$\frac{1}{3}$CE=4,根据勾股定理求出AC、AE,判断即可.
解答 解:∵△ABC的两条中线AD、CE交于点G,
∴点G是△ABC的重心,
∴AG=$\frac{2}{3}$AD=6,CG=$\frac{2}{3}$CE=8,EG=$\frac{1}{3}$CE=4,
∵AD⊥CE,
∴AC=$\sqrt{A{G}^{2}+C{G}^{2}}$=10,A正确;
AE=$\sqrt{A{G}^{2}+E{G}^{2}}$=2$\sqrt{13}$,
∴AB=2AE=4$\sqrt{13}$,B错误;
∵AD⊥CE,F是AC的中点,
∴GF=$\frac{1}{2}$AC=5,
∴BG=10,C正确;
BF=15,D正确,
故选:B.
点评 本题考查的是三角形的重心的概念和性质,三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:填空题
 把编号为1,2,3,4,…的若干盆花按下图所示摆放,花盆中的花按红、黄、蓝、紫的颜色依次循环排列,则第8行从左边数第6盆花的颜色为黄色色.
把编号为1,2,3,4,…的若干盆花按下图所示摆放,花盆中的花按红、黄、蓝、紫的颜色依次循环排列,则第8行从左边数第6盆花的颜色为黄色色.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
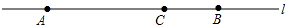 如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过2、10、$\frac{2}{3}$或$\frac{10}{3}$秒时线段PQ的长为6厘米.
如图,已知点A、点B是直线上的两点,AB=12厘米,点C在线段AB上,且AC=8厘米.点P、点Q是直线上的两个动点,点P的速度为1厘米/秒,点Q的速度为2厘米/秒.点P、Q分别从点C、点B同时出发,在直线上运动,则经过2、10、$\frac{2}{3}$或$\frac{10}{3}$秒时线段PQ的长为6厘米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②$\frac{FP}{PH}=\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.其中正确结论的序号是①③④.
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②$\frac{FP}{PH}=\frac{3}{5}$;③DP2=PH•PB;④tan∠DBE=2-$\sqrt{3}$.其中正确结论的序号是①③④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com