Question

16．如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H．给出下列结论：①△BDE∽△DPE；②$\frac{FP}{PH}=\frac{3}{5}$；③DP²=PH•PB；④tan∠DBE=2-$\sqrt{3}$．其中正确结论的序号是①③④．

Answer 1

分析 由正方形的性质和相似三角形的判定与性质，即可得出结论．

解答 解：∵△BPC是等边三角形，
∴BP=PC=BC，∠PBC=∠PCB=∠BPC=60°，
在正方形ABCD中，
∵AB=BC=CD，∠A=∠ADC=∠BCD=90°
∴∠ABE=∠DCF=30°，
∴∠CPD=∠CDP=75°，∴∠PDE=15°，
∵∠PBD=∠PBC-∠HBC=60°-45°=15°，
∴∠EBD=∠EDP，
∵∠DEP=∠DEB，
∴△BDE∽△DPE；故①正确；
∵PC=CD，∠PCD=30°，
∴∠PDC=75°，
∴∠FDP=15°，
∵∠DBA=45°，
∴∠PBD=15°，
∴∠FDP=∠PBD，
∵∠DFP=∠BPC=60°，
∴△DFP∽△BPH，
∴$\frac{PF}{PH}=\frac{DF}{PB}=\frac{DF}{CD}$=$\frac{\sqrt{3}}{3}$，故②错误；
∵∠PDH=∠PCD=30°，
∵∠DPH=∠DPC，
∴△DPH∽△CDP，
∴$\frac{PD}{CD}=\frac{PH}{PD}$，
∴PD²=PH•CD，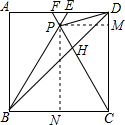
∵PB=CD，
∴PD²=PH•PB，故③正确；
如图，过P作PM⊥CD，PN⊥BC，
设正方形ABCD的边长是4，△BPC为正三角形，
∴∠PBC=∠PCB=60°，PB=PC=BC=CD=4，
∴∠PCD=30°
∴CM=PN=PB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$
PM=PC•sin30°=2，
∵DE∥PM，
∴∠EDP=∠DPM，
∴∠DBE=∠DPM，
∴tan∠DBE=tan∠DPM=$\frac{DM}{PM}$=$\frac{4-2\sqrt{3}}{2}$=2-$\sqrt{3}$，故④正确；
故答案为：①③④．

点评 本题考查的正方形的性质，相似三角形的判定和性质，平行线的性质，三角函数定义，等积变换，解答此题的关键是作出辅助线，利用锐角三角函数的定义求出PM及PN的长．