
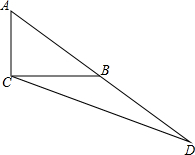
 如图,延长Rt△ABC斜边AB至D点,使BD=AB,连结CD,若cot∠BCD=2,求tanA的值.
如图,延长Rt△ABC斜边AB至D点,使BD=AB,连结CD,若cot∠BCD=2,求tanA的值. 分析 tan∠A的值可以转化为求直角三角形的比的问题,因而作DE⊥AC于E.在直角△AED中,根据三角函数的定义就可以求解.
解答 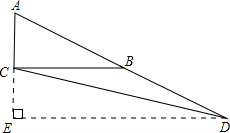 解:如图:做DE⊥AC于E,那么BC∥DE,△ABC∽△ADE.
解:如图:做DE⊥AC于E,那么BC∥DE,△ABC∽△ADE.
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$,
即$\frac{AB}{AB+BD}$=$\frac{AC}{AC+CE}$.
又由AB=BD,因此AC=CE.
根据BC⊥AC,∠BCE=90°,tan∠DCE=cot∠EDC=cot∠BCD=2,
直角三角形DCE中,tan∠DCE=$\frac{DE}{CE}$=2,
直角三角形ADE中,tan∠A=$\frac{DE}{AE}$=$\frac{DE}{2CE}$=1.
点评 本题涉及到三角形的中位线定理,锐角三角函数的定义,解答此题关键是作出辅助线构造直角三角形,再进行计算.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
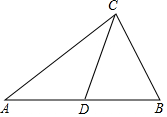 如图,已知CD是△ABC的边AB上的中线.
如图,已知CD是△ABC的边AB上的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com