
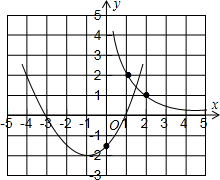
 如图,已知二次函数y=ax2+bx-
如图,已知二次函数y=ax2+bx-| 3 |
| 2 |
| 2 |
| x |
| 3 |
| 2 |
| k |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
|
|
| 1 |
| 2 |
| 3 |
| 2 |
|


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
 匀速地向如图的容器内注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化而变化,变化规律为一折线,下列图象(草图)正确的是( )
匀速地向如图的容器内注水,最后把容器注满,在注水过程中,水面的高度h随时间t的变化而变化,变化规律为一折线,下列图象(草图)正确的是( )A、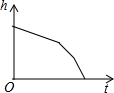 |
B、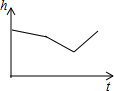 |
C、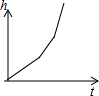 |
D、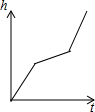 |
查看答案和解析>>
科目:初中数学 来源: 题型:
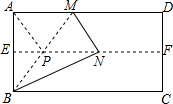 【问题提出】如果我们身边没有量角器和三角板,如何作15°大小的角呢?
【问题提出】如果我们身边没有量角器和三角板,如何作15°大小的角呢?查看答案和解析>>
科目:初中数学 来源: 题型:
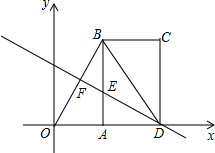 如图,在平面直角坐标系中,点A(1,0),点B(1,
如图,在平面直角坐标系中,点A(1,0),点B(1,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
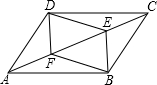 平行四边形ABCD中,E,F是对角线AC上两点,且∠ADF=∠CBE,连接DE,BF.
平行四边形ABCD中,E,F是对角线AC上两点,且∠ADF=∠CBE,连接DE,BF.查看答案和解析>>
科目:初中数学 来源: 题型:
| 海拔高度h(千米) | 0 | 1 | 2 | 3 | 4 | 5 | … |
| 气温t(℃) | 20 | 14 | 8 | 2 | -4 | -10 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com