
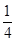 x2+
x2+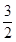 x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
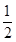 x﹣3;
x﹣3; ,﹣
,﹣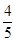 ).
).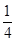 x2+
x2+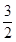 x﹣2=0,
x﹣2=0,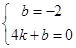 ,
,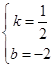 .
.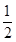 x﹣3;
x﹣3;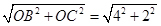 =2
=2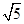 ,
,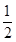 BC•FC=
BC•FC=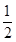 ×2
×2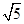 ×2
×2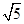 =10;
=10;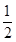 x﹣2=
x﹣2=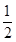 ×2﹣2=﹣1,
×2﹣2=﹣1,
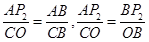 ,
,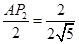 ,
,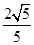 ,
,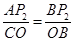 ,
,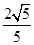 ×4=2BP2,
×4=2BP2,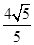 ,
,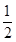 AB•QP2=
AB•QP2=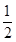 AP2•BP2,
AP2•BP2,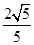 ×
×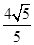 ,
,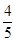 ,
,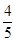 ,
, ,
, ,﹣
,﹣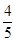 ),
), ,﹣
,﹣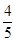 ).
).

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
 )三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
)三点,设点E(x,y)是抛物线上一动点,且在x轴下方,四边形OEBF是以OB为对角线的平行四边形.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
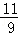 ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 x+m与抛物线y=
x+m与抛物线y= x2-2x+l交于不同的两点M、N(点M在点N的左侧).
x2-2x+l交于不同的两点M、N(点M在点N的左侧). x+m的交点为C,连结BM、BN,若S△MBC=
x+m的交点为C,连结BM、BN,若S△MBC= S△NBC,求直线MN的解析式;
S△NBC,求直线MN的解析式;
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com