
【题目】如图,每个小正方形的边长为1,A、B、C为小正方形的顶点,求证:∠ABC=45°. 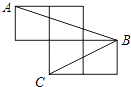
【答案】证明:连接AC,则由勾股定理可以得到:AC= ![]() ,BC=
,BC= ![]() ,AB=
,AB= ![]() . ∴AC2+BC2=AB2 .
. ∴AC2+BC2=AB2 .
∴△ABC是直角三角形.
又∵AC=BC,
∴∠CAB=∠ABC.
∴∠ABC=45°
【解析】连结AC,先依据勾股定理求得AB、AC、BC的长,然后依据勾股定理的逆定理可求得△ABC为直角三角形,然后依据AC=BC可得到三角形ABC为等腰直角三角形,故此可得到∠ABC=45°.
【考点精析】本题主要考查了等腰直角三角形和勾股定理的概念的相关知识点,需要掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】我市某工艺厂为配合伦敦奥运,设计了一款成本为20元/件的工艺品投入市场进行试销,得到如下数据:
销售单价x (元/件) | …… | 30 | 40 | 50 | 60 | …… |
每天销售量y(件) | …… | 500 | 400 | 300 | 200 | …… |
(1)把上表中x、y的各组对应值作为点的坐标,在右面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;

(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润为9000元?
(利润=销售总价-成本总价)
(3)根据要求,试销该工艺品每天获得的利润不低于8000元,每天销售量不低于350件,试确定销售单价x(元/件)的取值范围,并求出工艺厂试销该工艺品每天获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
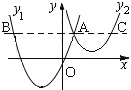
【题目】如图, 抛物线![]() 与
与![]() 交于点A
交于点A![]() ,过点A作
,过点A作![]() 轴的平行线,分别交两条抛物线于点B、C.则以下结论:① 无论
轴的平行线,分别交两条抛物线于点B、C.则以下结论:① 无论![]() 取何值,
取何值,![]() 的值总是正数;②
的值总是正数;② ![]() ;③ 当
;③ 当![]() 时,
时,![]() ;④ 当
;④ 当![]() >
>![]() 时,0≤
时,0≤![]() <1;⑤ 2AB=3AC.其中正确结论的编号是______________.
<1;⑤ 2AB=3AC.其中正确结论的编号是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( ) 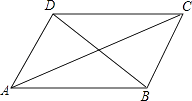
A.①②
B.②③
C.①③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,能够进入人体的肺部危害身体健康.检测PM2.5指数在一年中最可靠的一种观测方法是( )
A. 随机选择5天进行观测
B. 选择某个月进行连续观测
C. 选择在春节7天期间连续观测
D. 每个月都随机选中5天进行观测
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com