
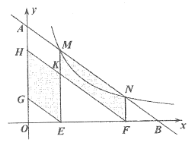
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于点
的图像交于点![]() 、
、![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() ,
,![]() ,分别交
,分别交![]() 轴于点
轴于点![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 和四边形
和四边形![]() 的面积和为12,则
的面积和为12,则![]() 的值为_______.
的值为_______.
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】抛物线M:y=ax2-4ax+a-1(a≠0)与x轴交于A,B两点(点A在点B左侧),抛物线的顶点为D.
(1)抛物线M的对称轴是直线______;
(2)当AB=2时,求抛物线M的函数表达式;
(3)在(2)的条件下,直线l:y=kx+b(k≠0)经过抛物线的顶点D,直线y=n与抛物线M有两个公共点,它们的横坐标分别记为x1,x2,直线y=n与直线l的交点的横坐标记为x3(x3>0),若当-2≤n≤-1时,总有x1-x3>x3-x2>0,请结合函数的图象,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
在数学中,当问题的条件不够时间,常添加辅助线构成新图形,形成新关系,建立已知与未知的桥梁,从而把原问题转化为易于解决的问题.在著名美籍匈牙利数学教波利亚所著的《数学的发现》一书中有这样一个例子:试作一个三角形,使它的三边长分别是各条中线长的三分之一,解决这个问题的步骤如下:

第一步,如图1,己知![]() 的三条中线
的三条中线![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() ,则有
,则有![]() .
.
下面是该结论的部分证明过程:

证明:如图1,过点![]() 作
作![]() 的平分线,交
的平分线,交![]() 的延长线于点
的延长线于点![]() ,则
,则![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
∵点![]() 是
是![]() 的中点,
的中点,
∴![]() .
.
……
第二步,同理可以证明:![]() .
.
第三步,如图2,取BM的中点![]() ,连接
,连接![]() .则
.则![]() 的三边长分别是各条中线长的三分之一.
的三边长分别是各条中线长的三分之一.
任务:(1)请在上面第一步中证明过程的基础上完成对结论![]() 的证明;
的证明;
(2)请完成第三步的结论的证明;
(3)请直接写出图2中![]() 与
与![]() 的面积比:
的面积比:![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的函数y=![]() +x,如表是y与x的几组对应值:
+x,如表是y与x的几组对应值:
x | … | ﹣4 | ﹣3 | -2 | - | -1 | - | - |
|
| 1 |
| 2 | 3 | 4 | … |
y | … | - | - | - | - | -2 | - | - |
|
| 2 |
|
|
|
| … |
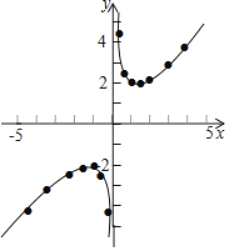
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点画出了此函数的图象请你根据学习函数的经验,根据画出的函数图象特征,对该函数的图象与性质进行探究:
(1)该函数的图象关于 对称;
(2)在y轴右侧,函数变化规律是当0<x<1,y随x的增大而减小;当x>1,y随x的增大而增大.在y轴左侧,函数变化规律是 .
(3)函数y=![]() 当x 时,y有最 值为 .
当x 时,y有最 值为 .
(4)若方程![]() +x=m有两个不相等的实数根,则m的取值范围是 .
+x=m有两个不相等的实数根,则m的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图Rt△ABC中,∠ACB=90°,AC=4,BC=2,点P在边AC上运动(点P与点A、C不重合).以P为圆心,PA为半径作⊙P交边AB于点D、过点D作⊙P的切线交射线BC于点E(点E与点B不重合).
(1)求证:BE=DE;
(2)若PA=1.求BE的长;
(3)在P点的运动过程中.(BE+PA)PA的值是否有最大值?如果有,求出最大值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
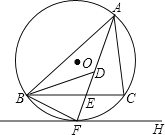
【题目】如图,⊙O是锐角△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.下列结论:①AF平分∠BAC;②点F为△BDC的外心;③![]() ;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是_____(把你认为正确结论的序号都填上).
;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是_____(把你认为正确结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com