
【题目】如图Rt△ABC中,∠ACB=90°,AC=4,BC=2,点P在边AC上运动(点P与点A、C不重合).以P为圆心,PA为半径作⊙P交边AB于点D、过点D作⊙P的切线交射线BC于点E(点E与点B不重合).
(1)求证:BE=DE;
(2)若PA=1.求BE的长;
(3)在P点的运动过程中.(BE+PA)PA的值是否有最大值?如果有,求出最大值;如果没有,请说明理由.

【答案】(1)证明见解析;(2)BE=3;(3)(BE+PA)PA有最大值,最大值为![]() .
.
【解析】
(1)由半径相等可设∠PAD=∠ADP=α,根据切线的性质得到∠EDP=90°,证明∠BDE=90°-α,由∠ACB=90°,得到∠B=90°﹣α,再根据“等角对等边”即可求解;
(2)过点E作EG⊥BD,则点G为BD的中点,根据等量代换得到∠GED=∠BAC,从而求出tan∠BAC![]() ,则cos∠BAC
,则cos∠BAC ![]() ,sin∠BAC
,sin∠BAC ![]() ,根据锐角三角函数的定义即可求出AD,DG以及BE;
,根据锐角三角函数的定义即可求出AD,DG以及BE;
(3)设PA=x,根据(2)可得出(BE+PA)PA=﹣2x2+5x,根据二次函数的性质即可求解.
解:(1)连接PD,∵PA=PD,
∴设∠PAD=∠ADP=α,
∵DE是圆的切线,则∠EDP=90°,
∴∠PDA+∠BDE=90°,即α+∠BDE=90°,
∴∠BDE=90°-α
∵∠ACB=90°,
∴∠B=90°﹣α,
∴∠BDE=∠B
∴BE=DE;
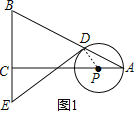
(2)过点E作EG⊥BD,则点G为BD的中点,
∵∠GED+∠EDB=90°,∠PDA+∠EDB=90°,
∴∠GED=∠PDA,
∴∠GED=∠BAC,
tan∠BAC![]() ,则cos∠BAC
,则cos∠BAC ![]() ,sin∠BAC
,sin∠BAC ![]() ,
,
∵PA=1,AC=4,BC=2,
∴AB=![]() ,
,
∴AD=2PAcos∠BAC ![]() ,
,
DG=BG![]() BD=(AB﹣AD)
BD=(AB﹣AD)![]() (2
(2![]() )
)![]() ,
,
BE=DE![]() 3,
3,
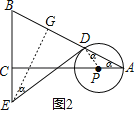
(3)设PA=x,
由(2)知:BE=DE=5﹣
则(BE+PA)PA=(5﹣2x+x)x=﹣x2+5x,
∵﹣1<0,故(BE+PA)PA有最大值,
∴当x![]() 时,有最大值为
时,有最大值为![]() .
.


科目:初中数学 来源: 题型:
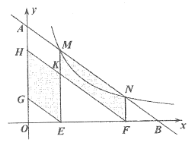
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图像交于点
的图像交于点![]() 、
、![]() ,与
,与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,作
,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,过点
,过点![]() 、
、![]() 分别作
分别作![]() ,
,![]() ,分别交
,分别交![]() 轴于点
轴于点![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 和四边形
和四边形![]() 的面积和为12,则
的面积和为12,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c为正数,若关于x的一元二次方程ax2+bx+c=0有两个实数根,则关于x的方程a2x2+b2x+c2=0解的情况为( )
A.有两个不相等的正根B.有一个正根,一个负根
C.有两个不相等的负根D.不一定有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到
两地同时出发,沿同一条公路相向行驶,相遇后,甲车继续以原速行驶到![]() 地,乙车立即以原速原路返回到
地,乙车立即以原速原路返回到![]() 地,甲、乙两车距
地,甲、乙两车距![]() 地的路程
地的路程![]() 与各自行驶的时间
与各自行驶的时间![]() 之间的关系如图所示.
之间的关系如图所示.
⑴![]() ________,
________,![]() ________;
________;
⑵求乙车距![]() 地的路程
地的路程![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
⑶当甲车到达![]() 地时,求乙车距
地时,求乙车距![]() 地的路程
地的路程
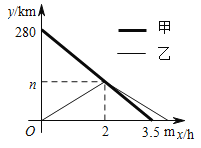
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不等实根x1、x2.
(1)求实数k的取值范围.
(2)若方程两实根x1、x2满足x1+x2=﹣x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“泥兴陶,,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:
(1)每只杯应降价多少元?
(2)在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com