
【题目】已知a、b、c为正数,若关于x的一元二次方程ax2+bx+c=0有两个实数根,则关于x的方程a2x2+b2x+c2=0解的情况为( )
A.有两个不相等的正根B.有一个正根,一个负根
C.有两个不相等的负根D.不一定有实数根
【答案】C
【解析】
由方程ax2+bx+c=0有两个实数根可得出b2﹣4ac≥0,结合a、b、c为正数可得出△=b4﹣4a2c2>0,进而可得出关于x的方程a2x2+b2x+c2=0有两个不相等的实数根,由根与系数的关系可得出该方程的两根之和为负、两根之积为正,进而可得出关于x的方程a2x2+b2x+c2=0有两个不相等的负根.
∵关于x的一元二次方程ax2+bx+c=0有两个实数根,
∴△=b2﹣4ac≥0.
又∵a、b、c为正数,
∴b2﹣4ac+2ac=b2﹣2ac>0,b2+2ac>0.
∵方程a2x2+b2x+c2=0的根的判别式△=b4﹣4a2c2=(b2+2ac)(b2﹣2ac)>0,
∴该方程有两个不相等的实数根.
设关于x的方程a2x2+b2x+c2=0的两个实数根为x1,x2,
则x1+x2=![]() <0,x1x2=
<0,x1x2=![]() >0,
>0,
∴关于x的方程a2x2+b2x+c2=0有两个不相等的负根.
故选C.


科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c经过点(1,2),(5,3),则下列说法正确的是( )
①抛物线与y轴有交点
②若抛物线经过点(2,2),则抛物线的开口向上
③抛物线的对称轴不可能是x=3
④若抛物线的对称轴是x=4,则抛物线与x轴有交点
A.①②③④B.①②③C.①③④D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
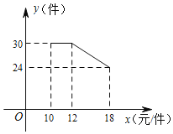
【题目】 某网店销售一种产品.这种产品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/件市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示:
(1)当12≤x≤18时,求y与x之间的函数关系式;
(2)求每天的销售利润w(元)与销售价x(元/件)之间的函数关系式并求出每件销售价为多少元时.每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=60°,AD平分∠BAC交边BC于点D,分别过D作DE∥AC交边AB于点E,DF∥AB交边AC于点F.
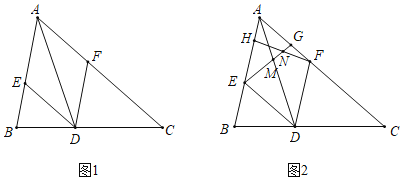
(1)如图1,试判断四边形AEDF的形状,并说明理由;
(2)如图2,若AD=4![]() ,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
(i)求ENEG的值;
(ii)将线段DM绕点D顺时针旋转60°得到线段DM′,求证:H,F,M′三点在同一条直线上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=﹣![]() x+m(m为常数)的图象与x轴交于A(﹣3,0),与y轴交于点C.以直线x=﹣1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.
x+m(m为常数)的图象与x轴交于A(﹣3,0),与y轴交于点C.以直线x=﹣1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a>0)经过A,C两点,与x轴正半轴交于点B.
(1)求一次函数及抛物线的函数表达式;
(2)P为线段AC上的一个动点(点P与C、A不重合)过P作x轴的垂线与这个二次函数的图象交于点D,连接CD,AD,点P的横坐标为n,当n为多少时,△CDA的面积最大,最大面积为多少?
(3)在对称轴上是否存在一点E,使∠ACB=∠AEB?若存在,求点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
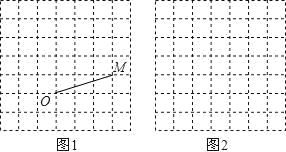
【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;
(2)在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com