
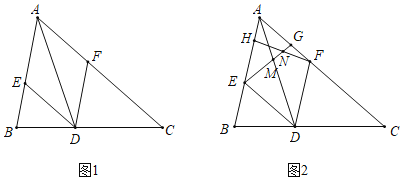
【题目】在△ABC中,∠BAC=60°,AD平分∠BAC交边BC于点D,分别过D作DE∥AC交边AB于点E,DF∥AB交边AC于点F.
(1)如图1,试判断四边形AEDF的形状,并说明理由;
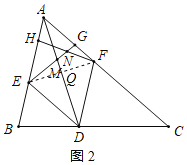
(2)如图2,若AD=4![]() ,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
,点H,G分别在线段AE,AF上,且EH=AG=3,连接EG交AD于点M,连接FH交EG于点N.
(i)求ENEG的值;
(ii)将线段DM绕点D顺时针旋转60°得到线段DM′,求证:H,F,M′三点在同一条直线上
【答案】(1) 四边形AEDF的形状是菱形,理由见解析;(1) (i) 12;(ii)见解析
【解析】
(1)由题意得出四边形AEDF是平行四边形;再根据角平分线性质及平行线性质可推出∠EAD=∠EDA;根据等角对等边得出AE=DE即可得出;
(2) (i) 连接EF交AD于点Q,根据菱形的性质得出△AEF是等边三角形,再根据余弦得出AE=AF=EF=4,根据SAS得出△AEG≌△EFH,根据全等三角形性质得出△AEG∽△NEH,最后根据相似三角形的性质得出答案;
(ii) 连接FM',根据等边三角形的性质及旋转的性质可得出△EDM≌△FDM',再根据全等三角形性质、等量代换即可得出答案.
(1)解:四边形AEDF的形状是菱形;理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DE∥AC,
∴∠EDA=∠FAD,
∴∠EAD=∠EDA,
∴AE=DE,
∴四边形AEDF是菱形;
(2)(i)解:连接EF交AD于点Q,如图2所示:
∵∠BAC=60°,四边形AEDF是菱形,
∴∠EAD=30°,AD、EF相互垂直平分,△AEF是等边三角形,
∴∠EAF=∠AEF=∠AFE=60°,
∵AD=![]() ,
,
∴AQ=![]() ,
,
在Rt△AQE中,cos∠EAQ=![]() ,即cos30°=
,即cos30°=![]() ,
,
∴AE=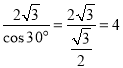 ,
,
∴AE=AF=EF=4,
在△AEG和△EFH中,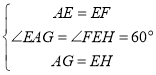 ,
,
∴△AEG≌△EFH(SAS),
∴∠AEG=∠EFH,
∴∠ENH=∠EFH+∠GEF=∠AEG+∠GEF=60°,
∴∠ENH=∠EAG,
∵∠AEG=∠NEH,
∴△AEG∽△NEH,
∴![]() ,
,
∴ENEG=EHAE=3×4=12;
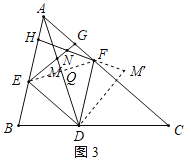
(ii)证明:如图3,连接FM',
∵DE∥AC,
∴∠AED=180°﹣∠BAC=120°,
由(1)得:△EDF是等边三角形,
∴DE=DF,∠EDF=∠FED=∠EFD=60°,
由旋转的性质得:∠MDM'=60°,DM=DM',
∴∠EDM=∠FDM',
在△EDM和△FDM'中,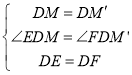 ,
,
∴△EDM≌△FDM'(SAS),
∴∠MED=∠DFM',
由(i)知,∠AEG=∠EFH,
∴∠DFM'+∠EFH=∠MED+∠AEG=∠AED=120°,
∴∠HFM
∴H,F,M′三点在同一条直线上.


科目:初中数学 来源: 题型:
【题目】我国为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.贫困户的生活条件得到改善,生活质量明显提高.恩施州为了全面了解贫困户对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
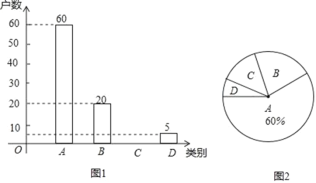
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,估计全州2000贫困户对扶贫工作基本满意及以上的大约多少户?
(3)恩施州扶贫办从利川市甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
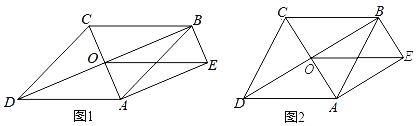
【题目】如图1,ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形ABCD是菱形;
(2)如图2,若∠ADC=60°,AD=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c为正数,若关于x的一元二次方程ax2+bx+c=0有两个实数根,则关于x的方程a2x2+b2x+c2=0解的情况为( )
A.有两个不相等的正根B.有一个正根,一个负根
C.有两个不相等的负根D.不一定有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步提高全民“节约用水”意识,某学校组织学生进行家庭月用水量情况调查活动,李明随机抽查了所住小区x户家庭的月用水量,绘制了下面不完整的统计图:

(1)求x并补全条形统计图;
(2)求这x户家庭的月平均用水量;并估计李明所住小区620户家庭中月用水量低于月平均用水量的家庭户数;
(3)从月用水量为5m3和9m3的家庭中任选两户进行用水情况问卷调查,求选出的两户中月用水量为5m3和9m3恰好各有一户家庭的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
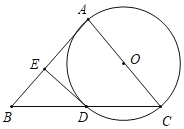
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC相交于点D,过点D作⊙O的切线与AB相交于点E.
(1)求证:DE⊥AB;
(2)若BE=2,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图象如图所示,与
的图象如图所示,与![]() 轴的交点分别
轴的交点分别![]() ,且函数与
,且函数与![]() 轴交点在
轴交点在![]() 的下方,现给以下结论:①
的下方,现给以下结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;④
;④![]() .则下列说法正确的是( )
.则下列说法正确的是( )

A.①②B.①③C.①④D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com