
ЁОЬтФПЁПЮвЙњЮЊСЫЪЕЯж2020ФъШЋУцЭбЦЖФПБъЃЌЪЕЪЉЁАОЋзМЗіЦЖЁБеНТдЃЌВЩШЁвьЕиАсЧЈЃЌВњвЕЗіГжЕШДыЪЉЃЎЦЖРЇЛЇЕФЩњЛюЬѕМўЕУЕНИФЩЦЃЌЩњЛюжЪСПУїЯдЬсИпЃЎЖїЪЉжнЮЊСЫШЋУцСЫНтЦЖРЇЛЇЖдЗіЦЖЙЄзїЕФТњвтЖШЧщПіЃЌНјааЫцЛњГщбљЕїВщЃЌЗжЮЊЫФИіРрБ№ЃКAЃЎЗЧГЃТњвтЃЛBЃЎТњвтЃЛCЃЎЛљБОТњвтЃЛDЃЎВЛТњвтЃЎвРОнЕїВщЪ§ОнЛцжЦГЩЭМ1КЭЭМ2ЕФЭГМЦЭМЃЈВЛЭъећЃЉЃЎ
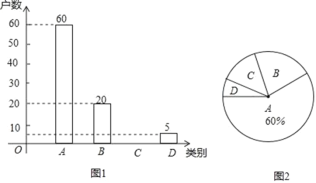
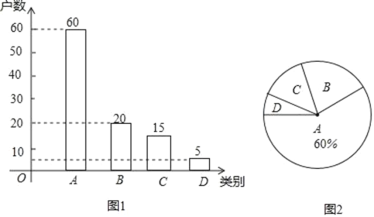
ИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉНЋЭМ1ВЙГфЭъећЃЛ
ЃЈ2ЃЉЭЈЙ§ЗжЮіЃЌЙРМЦШЋжн2000ЦЖРЇЛЇЖдЗіЦЖЙЄзїЛљБОТњвтМАвдЩЯЕФДѓдМЖрЩйЛЇ?
ЃЈ3ЃЉЖїЪЉжнЗіЦЖАьДгРћДЈЪаМзЯчеђ3ЛЇЁЂввЯчеђ2ЛЇЙВ5ЛЇЦЖРЇЛЇжаЃЌЫцЛњГщШЁСНЛЇНјааТњвтЖШЛиЗУЃЌЧѓетСНЛЇЦЖРЇЛЇЧЁКУЖМЪЧЭЌвЛЯчеђЕФИХТЪЃЎ
ЁОД№АИЁП(1) ВЙШЋЭМаЮМћНтЮіЃЛ(2) 1900ЛЇЃЛ (3)![]()
ЁОНтЮіЁП
(1)ЯШИљОнAЕФЛЇЪ§Г§вдЫљеМАйЗжБШЕУЕНБЛЕїВщЕФзмЛЇЪ§ЃЌдйЫуГіCЕФЛЇЪ§МДПЩВЙШЋЭМаЮЃЛ
(2)ЛљБОТњвтМАвдЩЯЪЧAЁЂBЁЂCШ§жжРраЭЃЌШ§жжРраЭЕФШЫЪ§Г§вдзмЕїВщШЫЪ§ЁС2000МДПЩЕУЕНД№АИЃЛ
(3) ЛЪїзДЭМСаГіЫљгаЕШПЩФмНсЙћЃЌдйИљОнИХТЪЙЋЪНЧѓНтПЩЕУЃЎ
НтЃК(1)ЁпБЛЕїВщЕФзмЛЇЪ§ЮЊ60ЁТ60%ЃН100ЃЌ
ЁрCРрБ№ЛЇЪ§ЮЊ100ЉЃЈ60+20+5ЃЉЃН15ЃЌ
ВЙШЋЭМаЮШчЯТЃК
ЃЈ2ЃЉЦЖРЇЛЇЖдЗіЦЖЙЄзїЕФТњвтЖШЪЧ![]() ЛЇЃЛ
ЛЇЃЛ
ЃЈ3ЃЉЛЪїзДЭМШчЯТЃК

гЩЪїзДЭМжЊЙВга20жжЕШПЩФмНсЙћЃЌЦфжаетСНЛЇЦЖРЇЛЇЧЁКУЖМЪЧЭЌвЛЯчеђЕФга8жжНсЙћЃЌ
ЫљвдетСНЛЇЦЖРЇЛЇЧЁКУЖМЪЧЭЌвЛЯчеђЕФИХТЪЮЊ![]() ЃН
ЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌAB=4ЃЌBC=2ЃЌе§ЗНаЮADEFЕФБпГЄЮЊ2ЃЌFЁЂAЁЂBдкЭЌвЛжБЯпЩЯЃЌе§ЗНаЮADEFЯђгвЦНвЦЕНЕуFгыBжиКЯЃЌЕуFЕФЦНвЦОрРыЮЊxЃЌЦНвЦЙ§ГЬжаСНЭМжиЕўВПЗжЕФУцЛ§ЮЊyЃЌдђyгыxЕФЙиЯЕЕФКЏЪ§ЭМЯѓБэЪОе§ШЗЕФЪЧЃЈ ЃЉ
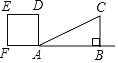
A.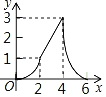 B.
B.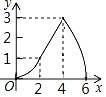
C.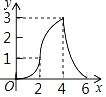 D.
D.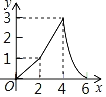
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
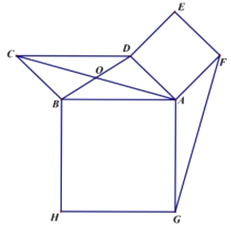
ЁОЬтФПЁПШчЭМЂйЃЌдкЕШбќШ§НЧаЮABCжаЃЌABЃНACЃН8ЃЌBCЃН14ЃЎШчЭМЂкЃЌдкЕзБпBCЩЯШЁвЛЕуDЃЌСЌНсADЃЌЪЙЕУЁЯDACЃНЁЯACDЃЎШчЭМЂлЃЌНЋЁїACDбизХADЫљдкжБЯпелЕўЃЌЪЙЕУЕуCТфдкЕуEДІЃЌСЌНсBEЃЌЕУЕНЫФБпаЮABEDЃЎдђBEЕФГЄЪЧ_____ЃЎ
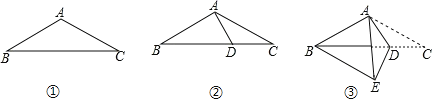
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкRtЁїABCКЭRtЁїABDжаЃЌЁЯACBЃН90ЁуЃЌЁЯABDЃН90ЁуЃЌABЃНBDЃЌBCЃН4ЃЌЃЈЕуAЁЂDЗжБ№дкжБЯпBCЕФЩЯЯТСНВрЃЉЃЌЕуGЪЧRtЁїABDЕФжиаФЃЌЩфЯпBGНЛБпADгкЕуEЃЌЩфЯпBCНЛБпADгкЕуFЃЎ
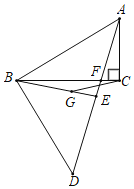
ЃЈ1ЃЉЧѓжЄЃКЁЯCAFЃНЁЯCBEЃЛ
ЃЈ2ЃЉЕБЕуFдкБпBCЩЯЃЌACЃН1ЪБЃЌЧѓBFЕФГЄЃЛ
ЃЈ3ЃЉШєЁїBGCЪЧвдBGЮЊбќЕФЕШбќШ§НЧаЮЃЌЪдЧѓACЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЦНааЫФБпаЮ![]() ЖдНЧЯп
ЖдНЧЯп![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() вд
вд![]() БпЗжБ№ЮЊБпГЄзїе§ЗНаЮ
БпЗжБ№ЮЊБпГЄзїе§ЗНаЮ![]() е§ЗНаЮ
е§ЗНаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧыЧѓГі
ЃЌЧыЧѓГі![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
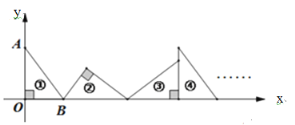
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌRtЁїABOЕФжБНЧЖЅЕуOдкдЕуЃЌAOдкyжсЩЯЃЌBOдкxжсЩЯЃЌЧвAO=4ЃЌBO=3ЃЌЁїABOШЦзХИїЖЅЕуЯђxжсе§ЗНЯђСЌајЗЙіЃЈЪМжеБЃГжвЛЬѕБпдкxжсЩЯЃЉЕУЕНЖрИіШ§НЧаЮЃЌЧыЮЪЕк2020ИіШ§НЧаЮЕФжБНЧЖЅЕузјБъЮЊ_________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=ax2+bx+cОЙ§ЕуЃЈ1ЃЌ2ЃЉЃЌЃЈ5ЃЌ3ЃЉЃЌдђЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
ЂйХзЮяЯпгыyжсгаНЛЕу
ЂкШєХзЮяЯпОЙ§ЕуЃЈ2ЃЌ2ЃЉЃЌдђХзЮяЯпЕФПЊПкЯђЩЯ
ЂлХзЮяЯпЕФЖдГЦжсВЛПЩФмЪЧx=3
ЂмШєХзЮяЯпЕФЖдГЦжсЪЧx=4ЃЌдђХзЮяЯпгыxжсгаНЛЕу
A.ЂйЂкЂлЂмB.ЂйЂкЂлC.ЂйЂлЂмD.ЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
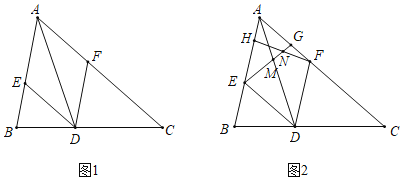
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯBAC=60ЁуЃЌADЦНЗжЁЯBACНЛБпBCгкЕуDЃЌЗжБ№Й§DзїDEЁЮACНЛБпABгкЕуEЃЌDFЁЮABНЛБпACгкЕуFЃЎ
(1)ШчЭМ1ЃЌЪдХаЖЯЫФБпаЮAEDFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
(2)ШчЭМ2ЃЌШєAD=4![]() ЃЌЕуHЃЌGЗжБ№дкЯпЖЮAEЃЌAFЩЯЃЌЧвEH=AG=3ЃЌСЌНгEGНЛADгкЕуMЃЌСЌНгFHНЛEGгкЕуNЃЎ
ЃЌЕуHЃЌGЗжБ№дкЯпЖЮAEЃЌAFЩЯЃЌЧвEH=AG=3ЃЌСЌНгEGНЛADгкЕуMЃЌСЌНгFHНЛEGгкЕуNЃЎ
(i)ЧѓENEGЕФжЕЃЛ
(ii)НЋЯпЖЮDMШЦЕуDЫГЪБеыа§зЊ60ЁуЕУЕНЯпЖЮDMЁфЃЌЧѓжЄЃКHЃЌFЃЌMЁфШ§ЕудкЭЌвЛЬѕжБЯпЩЯ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌABЪЧЁбOЕФжБОЖЃЌDЮЊЁбOЩЯвЛЕуЃЌODЁЭACЃЌДЙзуЮЊEЃЌСЌНгBD.
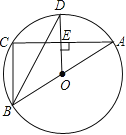
(1)ЧѓжЄЃКBDЦНЗжЁЯABCЃЛ
(2) ЕБЁЯODB=30ЁуЪБЃЌЧѓжЄЃКBC=OD.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com