
ЁОЬтФПЁП ФГЭјЕъЯњЪлвЛжжВњЦЗЃЎетжжВњЦЗЕФГЩБОМлЮЊ10дЊ/МўЃЌвбжЊЯњЪлМлВЛЕЭгкГЩБОМлЃЌЧвЮяМлВПУХЙцЖЈетжжВњЦЗЕФЯњЪлМлВЛИпгк18дЊ/МўЪаГЁЕїВщЗЂЯжЃЌИУВњЦЗУПЬьЕФЯњЪлСПyЃЈМўЃЉгыЯњЪлМлxЃЈдЊ/МўЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃК
ЃЈ1ЃЉЕБ12ЁмxЁм18ЪБЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓУПЬьЕФЯњЪлРћШѓwЃЈдЊЃЉгыЯњЪлМлxЃЈдЊ/МўЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНВЂЧѓГіУПМўЯњЪлМлЮЊЖрЩйдЊЪБЃЎУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
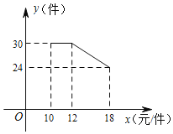
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx+42ЃЈ12ЁмxЁм18ЃЉЃЛЃЈ2ЃЉwЃН![]() ЃЌЕБxЃН18дЊЪБЃЎЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧ192дЊ
ЃЌЕБxЃН18дЊЪБЃЎЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧ192дЊ
ЁОНтЮіЁП
ЃЈ1ЃЉвРОнЬтвтЃЌИљОнЭМЯѓРћгУД§ЖЈЯЕЪ§ЗЈЃЌМДПЩЧѓЕУЯњЪлСПyЃЈМўЃЉгыЯњЪлМлxЃЈдЊ/МўЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃК
ЃЈ2ЃЉИљОнЯњЪлРћШѓ=ЯњЪлСПЁСЃЈЪлМл-НјМлЃЉЃЌСаГіУПЬьЕФЯњЪлРћШѓwЃЈдЊЃЉгыЯњЪлМлxЃЈдЊ/МўЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌдйвРОнКЏЪ§ЕФдіМѕадЧѓЕУзюДѓРћШѓЃЎ
НтЃКЃЈ1ЃЉвРЬтвтЃЌЩшyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЮЊЃКyЃНkx+b
НЋЕуЃЈ12ЃЌ30ЃЉЃЈ18ЃЌ24ЃЉДњШыЕУ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЁрЕБ12ЁмxЁм18ЪБЃЌ yгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃКyЃНЉx+42ЃЈ12ЁмxЁм18ЃЉ
ЃЈ2ЃЉвРЬтвтЃЌЕУwЃНyЃЈxЉ10ЃЉ
дђгаwЃН![]()
ЕБ10ЁмxЃМ12ЪБЃЌзюДѓРћШѓЮЊwЃН60дЊ
ЕБ12ЁмxЁм18ЪБЃЌ wЃНЉx2+52xЉ420ЃНЉЃЈxЉ26ЃЉ2+256
ЁпaЃНЉ1ЃМ0
ЁрХзЮяЯпПЊПкЯђЯТЃЌЙЪЕБ12ЁмxЁм18ЪБЃЌwЫцxЕФдіДѓЖјдіДѓ
ЁрЕБxЃН18ЪБЃЌгазюДѓжЕЕУwЃН192дЊ
ЙЪЕБxЃН18дЊЪБЃЎЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧ192дЊЃЌДЫЪБЯњЪлЕФМўЪ§ЮЊ24МўЃЎ


 аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ
аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИ
аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЦНУцжБНЧзјБъЯЕФкЕФЕуMТњзуКсЁЂзнзјБъЖМЮЊећЪ§ЃЌдђАбЕуMНазіЁАећЕуЁБЃЎР§ШчЃКPЃЈ1ЃЌ0ЃЉЁЂQЃЈ2ЃЌЉ2ЃЉЖМЪЧЁАећЕуЁБЃЎХзЮяЯпyЃНmx2Љ4mx+4mЉ2ЃЈmЃО0ЃЉгыxжсНЛгкЕуAЁЂBСНЕуЃЌШєИУХзЮяЯпдкAЁЂBжЎМфЕФВПЗжгыЯпЖЮABЫљЮЇГЩЕФЧјгђЃЈАќРЈБпНчЃЉЧЁгаЦпИіећЕуЃЌдђmЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A. ![]() ЁмmЃМ1B.
ЁмmЃМ1B. ![]() ЃМmЁм1C. 1ЃМmЁм2D. 1ЃМmЃМ2
ЃМmЁм1C. 1ЃМmЁм2D. 1ЃМmЃМ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЃЌbЃЌcЮЊГЃЪ§ЃЌЧвaЁй0ЃЉжаЕФxгыyЕФВПЗжЖдгІжЕШчБэЃК
x | Љ1 | 0 | 1 | 3 |
y | Љ1 | 3 | 5 | 3 |
ЯТСаНсТлДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
A.acЃМ0
B.ЕБxЃО1ЪБЃЌyЕФжЕЫцxЕФдіДѓЖјМѕаЁ
C.3ЪЧЗНГЬax2+ЃЈbЉ1ЃЉx+cЃН0ЕФвЛИіИљ
D.ЕБЉ1ЃМxЃМ3ЪБЃЌax2+ЃЈbЉ1ЃЉx+cЃО0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌABЁЮCDЃЌACЦНЗжЁЯBADЃЌCEЁЮADНЛABгкEЃЎ

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮAECDЪЧСтаЮЃЛ
ЃЈ2ЃЉШєЕуEЪЧABЕФжаЕуЃЌЪдХаЖЯЁїABCЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПзд2016ФъЙВЯэЕЅГЕЩЯЪавдРДЃЌИјШЫУЧЕФГіааЬсЙЉСЫБуРћЃЌЪмЕНСЫЙуДѓЪаУёЕФЧрэљЃЌФГЙЋЫОЮЊСЫСЫНтдБЙЄЩЯЯТАрЛиМвЕФТЗГЬЃЈЩшТЗГЬЮЊxЧЇУзЃЉЧщПіЃЌЫцЛњГщШЁСЫШєИЩУћдБЙЄНјааСЫЮЪОэЕїВщЃЌЯжНЋетаЉдБЙЄЕФЕїВщНсЙћЗжЮЊЫФИіЕШМЖЃЌAЃК0ЁмxЁм3ЃЛBЃК3ЃМxЁм6ЃЛCЃК6ЃМxЁм9ЃЛDЃКxЃО9ЃЛВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТСНЗљВЛЭъећЕФЭГМЦЭМЃК
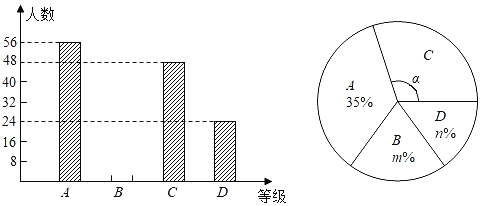
ЃЈ1ЃЉЧыВЙШЋЩЯУцЕФЬѕаЮЭГМЦЭМЃЌВЂЧѓmКЭnЕФжЕЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌЧѓЩШаЮЁАCЁБЫљЖдгІЕФдВаФНЧІСЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШєИУЙЋЫОга600УћдБЙЄЃЌЧыФуЙРМЦИУЙЋЫОТЗГЬдк6ЧЇУзвдЩЯбЁдёЙВЯэЕЅГЕЩЯЯТАрЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊaЁЂbЁЂcЮЊе§Ъ§ЃЌШєЙигкxЕФвЛдЊЖўДЮЗНГЬax2+bx+cЃН0гаСНИіЪЕЪ§ИљЃЌдђЙигкxЕФЗНГЬa2x2+b2x+c2ЃН0НтЕФЧщПіЮЊ(ЁЁЁЁ)
A.гаСНИіВЛЯрЕШЕФе§ИљB.гавЛИіе§ИљЃЌвЛИіИКИљ
C.гаСНИіВЛЯрЕШЕФИКИљD.ВЛвЛЖЈгаЪЕЪ§Иљ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЭМЯѓШчЭМЃЌЯТСаНсТлЃКЂйabc>0ЃЛЂк2a+b=0ЃЛЂлЕБmЁй1ЪБЃЌa+b>am2+bmЃЛЂмa-b+c>0ЃЛЂнШєax12+bx1=ax22+bx2ЃЌЧвx1Ёйx2ЃЌx1+x2=2ЃЎЦфжае§ШЗЕФгаЃЈ ЃЉ
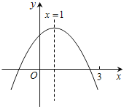
A.ЂкЂмB.ЂкЂнC.ЂйЂкЂлD.ЂкЂлЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌCDЃН4ЃЌЁЯCЃН90ЁуЃЌЕуBдкЯпЖЮCDЩЯЃЌ![]() ЃЌбиABЫљдкЕФжБЯпелЕўЁїACBЕУЕНЁїACЁфBЃЌШєЁїDCЁфBЪЧвдBC'ЮЊбќЕФЕШбќШ§НЧаЮЃЌдђЯпЖЮCBЕФГЄЮЊ_____ЃЎ
ЃЌбиABЫљдкЕФжБЯпелЕўЁїACBЕУЕНЁїACЁфBЃЌШєЁїDCЁфBЪЧвдBC'ЮЊбќЕФЕШбќШ§НЧаЮЃЌдђЯпЖЮCBЕФГЄЮЊ_____ЃЎ
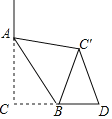
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌСтаЮOABCЕФвЛБпдкxжсЩЯЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓОЙ§СтаЮЖдНЧЯпЕФНЛЕуЃЌЧвгыABЫљдкжБЯпНЛгкЕуDЃЌвбжЊ
ЕФЭМЯѓОЙ§СтаЮЖдНЧЯпЕФНЛЕуЃЌЧвгыABЫљдкжБЯпНЛгкЕуDЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌдђвдЯТНсТлЃКЂй
ЃЌдђвдЯТНсТлЃКЂй![]() ЃЛЂкЕуDЕФзнзјБъЮЊ
ЃЛЂкЕуDЕФзнзјБъЮЊ![]() ЃЛЂл
ЃЛЂл![]() ЃЎЦфжае§ШЗЕФИіЪ§га
ЃЎЦфжае§ШЗЕФИіЪ§га![]()
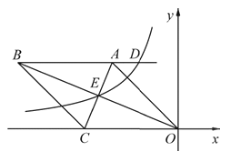
A.0ИіB.1ИіC.2ИіD.3Иі
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com