
【题目】如图,在平面直角坐标系中,菱形OABC的一边在x轴上,反比例函数![]() 的图象经过菱形对角线的交点,且与AB所在直线交于点D,已知
的图象经过菱形对角线的交点,且与AB所在直线交于点D,已知![]() ,
,![]() ,则以下结论:①
,则以下结论:①![]() ;②点D的纵坐标为
;②点D的纵坐标为![]() ;③
;③![]() .其中正确的个数有
.其中正确的个数有![]()
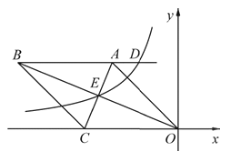
A.0个B.1个C.2个D.3个
【答案】C
【解析】
延长BA交y轴于点H,过点E作EF⊥OC于点F.①运用菱形的面积公式可求出△ECO的面积,根据△EFO的面积小于△ECO的面积可解决问题;②要求点D的纵坐标,只需根据菱形的面积公式(底乘以高)求出OH即可;③只需解直角三角形OHA,就可求出∠AOH,即可得到∠AOC,再根据菱形的性质,就可求出∠OBC.
解:延长BA交y轴于点H,过点E作EF⊥OC于点F,如图.
①∵四边形OABC是菱形,
∴S菱形OABC=![]() ACOB=
ACOB=![]() ×16
×16![]() =8
=8![]() ,
,
∴S△ECO=![]() S菱形OABC=2
S菱形OABC=2![]() ,
,
∴S△EFO=![]() OFEF=
OFEF=![]() (﹣k)<2
(﹣k)<2![]()
∴k>﹣4![]() .故①错误;
.故①错误;
②∵S菱形OABC=OCOH=8OH=8![]() ,
,
∴OH=2![]() ,故②正确;
,故②正确;
③在Rt△OHA中,
∵OA=OC=4,OH=2![]() ,
,
∴AH=2![]() =OH,
=OH,
∴∠AOH=∠OAH,
∵∠AHO=90°,
∴∠AOH=∠OAH=45°,
∴∠AOC=45°.
∵四边形OABC是菱形,
∴∠OBC=∠ABO=![]() ∠ABC=
∠ABC=![]() ∠AOC=22.5°,故③正确;
∠AOC=22.5°,故③正确;
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
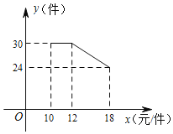
【题目】 某网店销售一种产品.这种产品的成本价为10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/件市场调查发现,该产品每天的销售量y(件)与销售价x(元/件)之间的函数关系如图所示:
(1)当12≤x≤18时,求y与x之间的函数关系式;
(2)求每天的销售利润w(元)与销售价x(元/件)之间的函数关系式并求出每件销售价为多少元时.每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
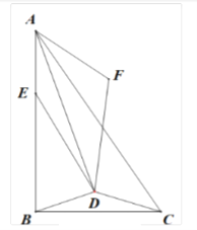
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内一个动点,且满足
内一个动点,且满足![]() ,当线段
,当线段![]() 取最小值时,记
取最小值时,记![]() ,线段
,线段![]() 上一动点
上一动点![]() 绕着点
绕着点![]() 顺时针旋转得到点
顺时针旋转得到点![]() ,且满足
,且满足![]() ,则
,则![]() 的最小值为 _____________
的最小值为 _____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,橫、纵坐标都是整数的点叫做整点.直线y=ax与抛物线y=ax2﹣2ax﹣1(a≠0)围成的封闭区域(不包含边界)为W.
(1)求抛物线顶点坐标(用含a的式子表示);
(2)当a=![]() 时,写出区域W内的所有整点坐标;
时,写出区域W内的所有整点坐标;
(3)若区域W内有3个整点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人口数据又称为人口统计数据,是指国家和地区的相关人口管理部门通过户口登记、人口普査等方式统计得出的相关数据汇总.人口数据对国家和地区的人口状况、管理以及各项方针政策的制定都具有重要的意义.下面是关于人口数据的部分信息.
a.2018年中国大陆(不含港澳台)31个地区人口数量(单位:千万人)的频数分布直方图(数据分成6组:0≤x<2,2≤x<4,4≤x<6,6≤x<8,8≤x<10,10≤x≤12):
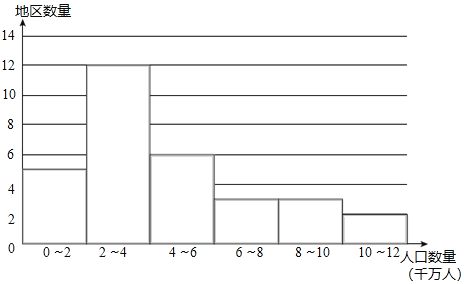
b.人口数量在2≤x<4这一组的是:
2.2 2.4 2.5 2.5 2.6 2.7 3.1 3.6 3.7 3.8 3.9 3.9
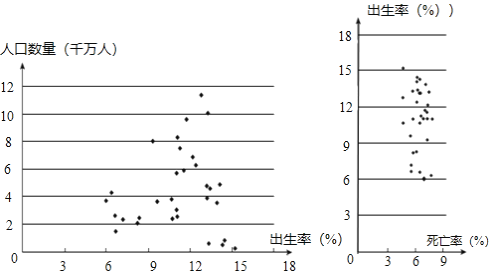
c.2018年中国大陆(不含港澳台)31个地区人口数量(单位:千万人)、出生率(单位:‰)、死亡率(单位:‰)的散点图:
d.如表是我国三次人口普查中年龄结构构成情况:
0~14岁人口比例 | 15~59岁人口比例 | 60岁以上人口比例 | |
第二次人口普查 | 40.4% | 54.1% | 5.5% |
第五次人口普查 | 22.89% | 66.78% | 10.33% |
第六次人口普查 | 16.6% | 70.14% | 13.26% |
e.世界各国的人口出生率差别很大,出生率可分为五等,最高>50‰,最低<20‰,2018年我国人口出生率降低至10.94‰,比2017年下降1.43个千分点.
根据以上信息,回答下列问题:
(1)2018年北京人口为2.2千万人,我国大陆(不含港澳台)地区中,人口数量从低到高排列,北京排在第 位.
(2)人口增长率=人口出生率﹣人口死亡率,我国大陆(不含港澳台)地区中人口在2018年出现负增长的地区有 个,在这些地区中,人口数量最少的地区人数为 千万人(保留小数点后一位).
(3)下列说法中合理的是 .
①我国人口基数较大,即使是人口出生率和增长率都缓慢增长的前提下,人口总数仍然是在不断攀升的,所以我国计划生育的基本国策是不变的;
②随着我国老龄化越来越严重,所以出台了“二孩政策”,目的是为了缓解老龄化的压力.
查看答案和解析>>
科目:初中数学 来源: 题型:
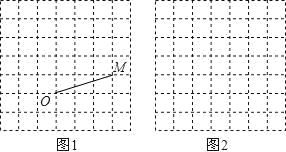
【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;
(2)在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一所中学九年级240名同学参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树数量,所分四个类别为,A:植4棵;B:植5棵;C:植6棵;D:植7棵.将各类别人数绘制成扇形图和条形图.经确认扇形图是正确的,而条形图尚有一处错误.
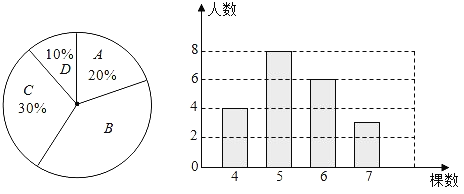
(1)指出条形图中存在的错误,并说明理由.
(2)指出样本的众数、中位数.
(3)估计在全年级随机抽取1人,植树5棵的概率.
(4)估计全年级240名同学这次共植树多少棵.(精确到10棵)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件,如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若在销售过程中每一件商品有a(a>1)元的其他费用,商家发现当售价每件不低于57元时,每月的销售利润随x的增大而减小,请直接写出a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com