
【题目】(阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,
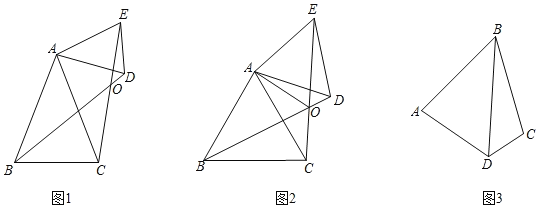
如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(材料理解)(1)在图1中证明小明的发现.
(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有 .(将所有正确的序号填在横线上).
(延伸应用)(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
【答案】(1)证明见解析;(2)①②③;(3)∠A+∠C=180°.
【解析】
(1)利用等式的性质得出∠BAD=∠CAE,即可得出结论;
(2)同(1)的方法判断出△ABD≌△ACE,得出BD=CE,再利用对顶角和三角形的内角和定理判断出∠BOC=60°,再判断出△BCF≌△ACO,得出∠AOC=120°,进而得出∠AOE=60°,再判断出BF<CF,进而判断出∠OBC>30°,即可得出结论;
(3)先判断出△BDP是等边三角形,得出BD=BP,∠DBP=60°,进而判断出△ABD≌△CBP(SAS),即可得出结论.
(1)证明:∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
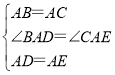 ,
,
∴△ABD≌△ACE;
(2)如图2,

∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
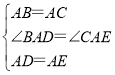 ,
,
∴△ABD≌△ACE,
∴BD=CE,①正确,∠ADB=∠AEC,
记AD与CE的交点为G,
∵∠AGE=∠DGO,
∴180°-∠ADB-∠DGO=180°-∠AEC-∠AGE,
∴∠DOE=∠DAE=60°,
∴∠BOC=60°,②正确,
在OB上取一点F,使OF=OC,
∴△OCF是等边三角形,
∴CF=OC,∠OFC=∠OCF=60°=∠ACB,
∴∠BCF=∠ACO,
∵AB=AC,
∴△BCF≌△ACO(SAS),
∴∠AOC=∠BFC=180°-∠OFC=120°,
∴∠AOE=180°-∠AOC=60°,③正确,
连接AF,要使OC=OE,则有OC=![]() CE,
CE,
∵BD=CE,
∴CF=OF=![]() BD,
BD,
∴OF=BF+OD,
∴BF<CF,
∴∠OBC>∠BCF,
∵∠OBC+∠BCF=∠OFC=60°,
∴∠OBC>30°,而没办法判断∠OBC大于30度,
所以,④不一定正确,
即:正确的有①②③,
故答案为①②③;
(3)如图3,
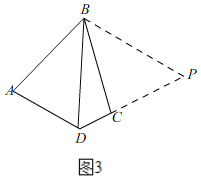
延长DC至P,使DP=DB,
∵∠BDC=60°,
∴△BDP是等边三角形,
∴BD=BP,∠DBP=60°,
∵∠BAC=60°=∠DBP,
∴∠ABD=∠CBP,
∵AB=CB,
∴△ABD≌△CBP(SAS),
∴∠BCP=∠A,
∵∠BCD+∠BCP=180°,
∴∠A+∠BCD=180°.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形 ABCD 中,AD∥BC,AB=BC=CD=AD=4,∠A=∠C=60°,连接 BD,将△BCD 绕点 B 旋转,当 BD(即 BD′)与 AD 交于一点 E,BC(即 BC′)同时与 CD 交于一点 F 时,下列结论正确的是( )
①AE=DF;②∠BEF=60°;③∠DEB=∠DFB;④△DEF 的周长的最小值是4+2![]()
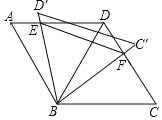
A. ①② B. ②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
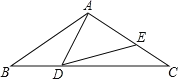
【题目】如图,在△ABC中,AB=AC=2,∠B=36°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=36°,DE交线段AC于点E.
(1)当∠BDA=128°时,∠EDC= ,∠AED= ;
(2)线段DC的长度为何值时,△ABD≌△DCE?请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
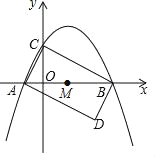
【题目】如图,抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴相交于点C.
(1)求抛物线的解析式;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
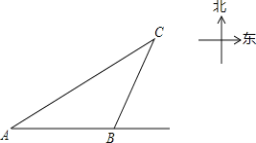
【题目】如图,一艘轮船由西向东航行,在![]() 处测得北偏东
处测得北偏东![]() 反向有小岛
反向有小岛![]() ,继续前进
,继续前进![]() 海里到达
海里到达![]() 处,此时测得小岛
处,此时测得小岛![]() 在船的北偏东
在船的北偏东![]() 方向,则船继续向东航行________海里,离小岛最近(精确到
方向,则船继续向东航行________海里,离小岛最近(精确到![]() 海里,参考数据
海里,参考数据![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年我市某水果销售公司购进了国外种植的一种水果,在四月份进行了一个月(30 天)的试销,购进价格为 20 元/公斤,销售结束后,发现日销售量 P(公斤)与销售时间 x(天)之间 关系如下列表格:(1≤x≤30,且 x 为整数)且后 10 天的销售价格 Q(元/公斤)与销售时间 x(天)之间有如下关系:Q=x+20(21≤x≤30,且 x 为整数),

(1)观察表格,请用你所学过的一次函数、二次函数和反比例函数的有关知识写出 P 与 x 所满足的函数关系式,并求出四月份后十天中日销售利润 W 的最大值;
(2)进入五月份,这种水果在台湾大量上市,受此影响这种水果的购进价格每公斤降低了 5 元,同时公司也加大了宣传力度,结果五月份第一天的销售量比上一个月最后一天的销售量增加了 a%,同时价格也比上一个月最后一天的价格增加了 0.4a%,结果在五月的第一天就获得了 1600 元的利润,请参考一下数据,估算 a 的整数值.(参考数据:152=225,162=256,172=289)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:A、F、C、D四点在一条直线上,AF=CD,∠D=∠A,且AB=DE.请将下面说明△ABC≌△DEF的过程和理由补充完整.
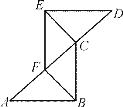
解:∵AF=CD(______)
∴AF+FC=CD+_____,即AC=DF,
在△ABC和△DEF中:AC=______(已知),∠D=∠A(________),AB=______(已知),
∴△ABC≌△DEF(_______)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com