
【题目】去年我市某水果销售公司购进了国外种植的一种水果,在四月份进行了一个月(30 天)的试销,购进价格为 20 元/公斤,销售结束后,发现日销售量 P(公斤)与销售时间 x(天)之间 关系如下列表格:(1≤x≤30,且 x 为整数)且后 10 天的销售价格 Q(元/公斤)与销售时间 x(天)之间有如下关系:Q=x+20(21≤x≤30,且 x 为整数),

(1)观察表格,请用你所学过的一次函数、二次函数和反比例函数的有关知识写出 P 与 x 所满足的函数关系式,并求出四月份后十天中日销售利润 W 的最大值;
(2)进入五月份,这种水果在台湾大量上市,受此影响这种水果的购进价格每公斤降低了 5 元,同时公司也加大了宣传力度,结果五月份第一天的销售量比上一个月最后一天的销售量增加了 a%,同时价格也比上一个月最后一天的价格增加了 0.4a%,结果在五月的第一天就获得了 1600 元的利润,请参考一下数据,估算 a 的整数值.(参考数据:152=225,162=256,172=289)
【答案】(1)答案见解析 (2)63
【解析】
(1)设P与x之间的函数关系式为y=kx+b,将9(1,78),(2,76)代入关系式就可以求出结论;由日销售利润=每天的销售量×每公斤的利润就可以分别表示出W与x的关系;
(2)先分别求出5月份第一的进价,第一天的销售量,销售价格,同样由日销售利润=每天的销售量×每公斤的利润建立方程求出其解即可.
解:(1)设 P 与 x 之间的函数关系式为 y=kx+b,由题意,得![]() ,解得:
,解得:![]() ,
,
∴P=﹣2x+80;
(2)W=(Q﹣20)P,
=(x+20﹣20)(﹣2x+80),
=﹣2x2+80x(21≤x≤30,且x为整数),
∴抛物线的对称轴x=20.
又∵21≤x≤30,且 x为整数,
∴当 x=21 时,W 有最大值,最大值=798.
(3)当 x= 30 时,P=20,Q2=50,
则 20(1+a%)〔50(1+0.4 a%)﹣15〕=1600,设 a%=m,则20(1+m)(50+20m﹣15)= 1600,即 4m2+11m﹣9=0,
m=![]() ,
,
∵162=256
∴m=﹣![]() (舍去)或 m=
(舍去)或 m=![]() =0.625,即整数 a 的值为 63.
=0.625,即整数 a 的值为 63.


科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC 中,AD 是 BC 边上的中线.
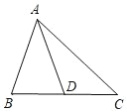
(1)画出与△ACD 关于点 D 成中心对称的三角形;
(2)找出与 AC 相等的线段;
(3)探索:△ABC 中,AB+AC 与中线 AD 之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
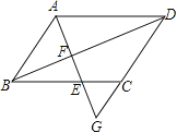
【题目】如图,在平行四边形ABCD中,点G在边DC的延长线上,AG交边BC于点E,交对角线BD于点F.
(1)求证:AF2=EFFG;
(2)如果EF=![]() ,FG=
,FG=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材科)小明同学发现这样一个规律:两个顶角相等的等腰三角形,
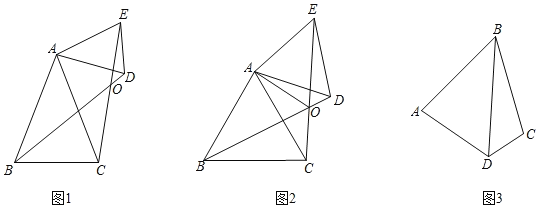
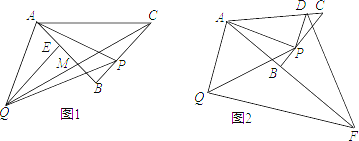
如果具有公共的项角的顶点,并把它们的底角顶点连接起来则形成一组全等的三角形,小明把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小明发现若∠BAC=∠DAE,AB=AC,AD=AE,则△ABD≌△ACE.
(材料理解)(1)在图1中证明小明的发现.
(深入探究)(2)如图2,△ABC和△AED是等边三角形,连接BD,EC交于点O,连接AO,下列结论:①BD=EC;②∠BOC=60°;③∠AOE=60°;④EO=CO,其中正确的有 .(将所有正确的序号填在横线上).
(延伸应用)(3)如图3,AB=BC,∠ABC=∠BDC=60°,试探究∠A与∠C的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
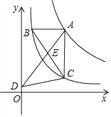
【题目】如图,点A是反比例函数y=![]() 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=![]() 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 重合),以
重合),以![]() 为腰长作等腰直角
为腰长作等腰直角![]() ,
,![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
(3)如图2,过![]() 作
作![]() 于
于![]() 的延长线于点
的延长线于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时(不与
上运动时(不与![]() 重合),式子
重合),式子![]() 的值会变化吗?若不变,求出该值;若变化,请说明理由..
的值会变化吗?若不变,求出该值;若变化,请说明理由..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨9 000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售,当大部分干果售出后,余下的600 kg按售价的八折售完.
(1)该种干果第一次的进价是多少?
(2)超市销售这种干果共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
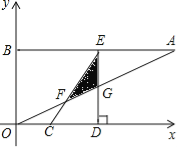
【题目】如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD=![]() ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t的函数关系式及t的取值范围;
(3)连结DF,
①当t取何值时,有![]() ?
?
②直接写出ΔCDF的外接圆与OA相切时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
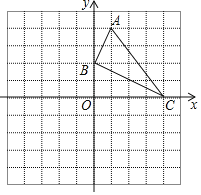
【题目】如图,已知网格上最小的正方形的边长为![]() (长度单位),点
(长度单位),点![]() 在格点上.
在格点上.
(1)直接在平面直角坐标系中作出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() (点
(点![]() 对应点
对应点![]() ,点
,点![]() 对应点
对应点![]() );
);
(2)![]() 的面积为 (面积单位)(直接填空);
的面积为 (面积单位)(直接填空);
(3)点![]() 到直线
到直线![]() 的距离为 (长度单位)(直接填空);
的距离为 (长度单位)(直接填空);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com