
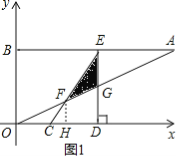
【题目】如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD=![]() ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
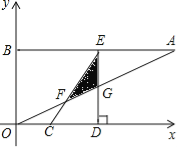
(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t的函数关系式及t的取值范围;
(3)连结DF,
①当t取何值时,有![]() ?
?
②直接写出ΔCDF的外接圆与OA相切时t的值.
【答案】(1)线段CE的长为![]() ;
;
(2)S=![]() (
(![]() ﹣t)2,t的取值范围为:0≤t≤
﹣t)2,t的取值范围为:0≤t≤![]() ;
;
(3)①当t=![]() 时,DF=CD;②ΔCDF的外接圆与OA相切时t=
时,DF=CD;②ΔCDF的外接圆与OA相切时t=![]() .
.
【解析】
试题(1)直接根据勾股定理求出CE的长即可;
(2)作FH⊥CD于H.,由AB∥OD,DE⊥OD,OB⊥OD可知四边形ODEB是矩形,故可用t表示出AE及BE的长,由相似三角形的判定定理可得出△OCF∽△AEF,△ODG∽△AEG,由相似三角形的性质可用t表示出CF及EG的长,FH∥ED可求出HD的长,由三角形的面积公式可求出S与t的关系式;
(3)①由(2)知CF=t,当DF=CD时,作DK⊥CF于K,则CK=![]() CF=
CF=![]() t,CK=CDcos∠DCE,由此可得出t的值;
t,CK=CDcos∠DCE,由此可得出t的值;
②先根据勾股定理求出OA的长,由(2)知HD=![]() (5﹣t),由相似三角形的判定定理得出Rt△AOB∽Rt△OFH,可用t表示出OF的长,因为当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,由切割线定理可知OF2=OCOD,故可得出结论.
(5﹣t),由相似三角形的判定定理得出Rt△AOB∽Rt△OFH,可用t表示出OF的长,因为当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,由切割线定理可知OF2=OCOD,故可得出结论.
试题解析:(1)∵在Rt△CDE中,CD=![]() ,DE=2,
,DE=2,
∴CE=![]() ;
;
(2)如图1,作FH⊥CD于H.
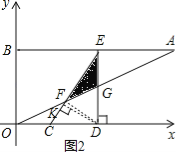
∵AB∥OD,DE⊥OD,OB⊥OD,
∴四边形ODEB是矩形,
∴BE=OD,
∵OC=t,
∴BE=OD=OC+CD=t+![]() ,
,
∴AE=AB﹣BE=4﹣(t+![]() )=
)=![]() ﹣t,
﹣t,
∵AB∥OD,
∴△OCF∽△AEF,△ODG∽△AEG,
∴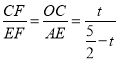 ,
,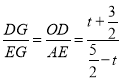 ,
,
又∵CF+EF=5,DG+EG=4,
∴![]() ,
,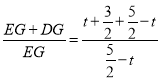 ,
,
∴CF=t,EG=![]() ,
,
∴EF=CE﹣CF=5﹣t,
∵FH∥ED,
∴![]() CD=
CD=![]() (
(![]() ﹣t),
﹣t),
∴S=![]() EGHD=
EGHD=![]() ×
×![]() ×
×![]() (
(![]() ﹣t)=
﹣t)=![]() (
(![]() ﹣t)2,
﹣t)2,
t的取值范围为:0≤t≤![]() ;
;
(3)①由(2)知CF=t,
如图2,当DF=CD时,如图作DK⊥CF于K,
则CK=![]() CF=
CF=![]() t,
t,
∵CK=CDcos∠DCE,
∴![]() t=3×
t=3×![]() ,
,
解得:t=![]() ;
;
∴当t=![]() 时,DF=CD;
时,DF=CD;
②∵点A,B坐标分别为(8,4),(0,4),
∴AB=8,OB=4,
∴OA=![]() =4
=4![]() ,
,
∵由(2)知HD=![]() (5﹣t),
(5﹣t),
∴OH=t+3﹣![]() (5﹣t)=
(5﹣t)=![]() ,
,
∵∠A+∠AOB=∠AOD+∠AOB=90°,
∴∠A=∠AOD,
∴Rt△AOB∽Rt△OFH,
∴![]() ,
,
解得OF=![]() ,
,
∵当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,
∴OF2=OCOD,即(![]() )2=t(t+3),得t=
)2=t(t+3),得t=![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
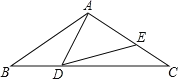
【题目】如图,在△ABC中,AB=AC=2,∠B=36°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=36°,DE交线段AC于点E.
(1)当∠BDA=128°时,∠EDC= ,∠AED= ;
(2)线段DC的长度为何值时,△ABD≌△DCE?请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年我市某水果销售公司购进了国外种植的一种水果,在四月份进行了一个月(30 天)的试销,购进价格为 20 元/公斤,销售结束后,发现日销售量 P(公斤)与销售时间 x(天)之间 关系如下列表格:(1≤x≤30,且 x 为整数)且后 10 天的销售价格 Q(元/公斤)与销售时间 x(天)之间有如下关系:Q=x+20(21≤x≤30,且 x 为整数),

(1)观察表格,请用你所学过的一次函数、二次函数和反比例函数的有关知识写出 P 与 x 所满足的函数关系式,并求出四月份后十天中日销售利润 W 的最大值;
(2)进入五月份,这种水果在台湾大量上市,受此影响这种水果的购进价格每公斤降低了 5 元,同时公司也加大了宣传力度,结果五月份第一天的销售量比上一个月最后一天的销售量增加了 a%,同时价格也比上一个月最后一天的价格增加了 0.4a%,结果在五月的第一天就获得了 1600 元的利润,请参考一下数据,估算 a 的整数值.(参考数据:152=225,162=256,172=289)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
①16a﹣4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③a=﹣
,y2)是函数图象上的两点,则y1>y2;③a=﹣![]() c;④若△ABC是等腰三角形,则b=﹣
c;④若△ABC是等腰三角形,则b=﹣![]() .其中正确的有______(请将结论正确的序号全部填上)
.其中正确的有______(请将结论正确的序号全部填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张月历表,在此月历表上用一个正方形任意圈出 2×2个数(如 1,2,8,9), 如果圈出的四个数中的最小数与最大数的积为 308,那么这四个数的和为( )
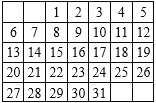
A.68B.72C.74D.76
查看答案和解析>>
科目:初中数学 来源: 题型:
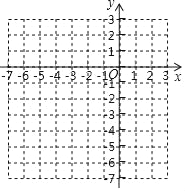
【题目】如图所示,在平面直角坐标系中有一格点三角形,该三角形的三个顶点为:A(1,1),B(﹣3,1),C(﹣3,﹣1).
(1)画出△ABC的外接圆⊙P;
(2)在如图所示的网格线内,以坐标原点O点为位似中心,将△ABC按位似比为2:1放大,A、B、C的对应点分别为A′、B′、C′,将△A′B′C′沿x轴方向如何平移,使B′C′所在的直线与⊙P相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:A、F、C、D四点在一条直线上,AF=CD,∠D=∠A,且AB=DE.请将下面说明△ABC≌△DEF的过程和理由补充完整.
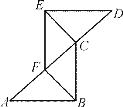
解:∵AF=CD(______)
∴AF+FC=CD+_____,即AC=DF,
在△ABC和△DEF中:AC=______(已知),∠D=∠A(________),AB=______(已知),
∴△ABC≌△DEF(_______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com